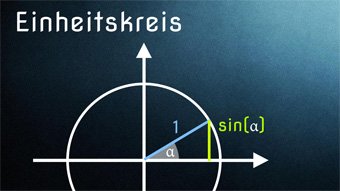
Die zuvor kennengelernte Identität sin(α) = cos(90°- α) verrät, dass der Kosinus der Sinus des Komplimentärwinkels ist.
Dies können wir uns noch einmal am rechtwinkligen Dreieck ansehen:
\( \sin(β) = \frac{b}{c} \\ \cos(α) = \frac{b}{c} \\ \longrightarrow \sin(β) = \cos(α) \)
Wenn die Hypotenuse 1 ist, dann erhalten wir:
\( \sin(β) = \frac{b}{1} = b \\ \cos(α) = \frac{b}{1} = b \\ \longrightarrow \sin(β) = \cos(α) = b \)
Der Winkel α ist Komplementärwinkel zu Winkel β, das heißt, beide ergeben immer zusammen 90°.
Also α + β = 90° bzw. α = 90° - β.
Das können wir einsetzen und erhalten:
sin(β) = cos(α) = b
sin(β) = cos(90° - β) = b
Genauso:
cos(β) = sin(α)
cos(β) = sin(90° - β)
Wir erkennen:
Der Kosinuswert von β ist der Sinuswert des Komplementärwinkels α. – Der KoSinus.