Eine „Funktion“ ist die eindeutige Zuordnung von einem Wert zu einem anderen Wert. Dabei ist der eine Wert von dem anderen Wert abhängig (es ergibt sich ein Wertepaar).
Darstellungen von Funktionen
Eine Funktion (auch „Zuordnung“ oder „Abbildung“) kann in verschiedenen Weisen dargestellt werden.
Ein paar Beispiele von Darstellungsarten:
Tabellarische Darstellung (Wertetabelle)
Eine Wertetabelle ist eine Tabelle, die Paare von Werten auflistet.
Bei einer Funktion muss jedem x-Wert genau ein y-Wert zugeordnet sein.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -7,5 | -5 | -2,5 | 0 | 2,5 | 5 | 7,5 |
Zeichnerische Darstellung (Graph)
Die Wertepaare einer Funktion können als Punkte im Koordinatensystem dargestellt werden. Dabei deutet man den zusammenhängenden x- und y-Wert als Koordinaten eines Punktes.
| x | y | Punkt |
| -3 | -7,5 | P(-3|-7,5) |
| -2 | -5 | P(-2|-5) |
| -1 | -2,5 | P(-1|-2,5) |
| 0 | 0 | P(0|0) |
| 1 | 2,5 | P(1|2,5) |
| 2 | 5 | P(2|5) |
| 3 | 7,5 | P(3|7,5) |
Pfeildiagramm (x → y)
Eine Zuordnung kann auch über ein Pfeildiagramm erfolgen. Dabei zeichnen wir Pfeile (Verbindungen) von einer Menge zu einer anderen:
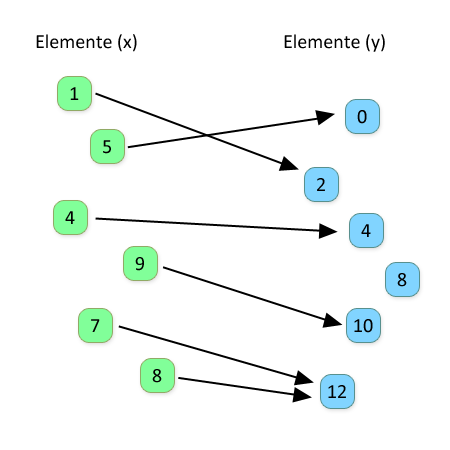
Mengen-Darstellung
Eine Zuordnung kann auch als Menge notiert werden. Beispiel:
M = { (-1|1), (0|0), (2|4) }
Hier haben wir die Menge M, die drei Wertepaare enthält.
Analytische Darstellung (Gleichung)
Eine Funktion kann in Form einer Gleichung notiert werden:
f(x) = 2,5·x = y
Wir sprechen dann von einer „Funktionsgleichung“ (also die Gleichung einer Funktion).
f ist der Name der Funktion. f(x) heißt „f von x“ und gibt den Funktionswert y an der Stelle x an. Der Funktionswert y berechnet sich durch eine Formel (im Beispiel 2,5·x).
Wir setzen also in die Funktionsgleichung einen Wert für x ein und durch die Formel berechnen wir den passenden Wert für y:
f(x) = 2,5·x = y
Für zum Beispiel x = 4 ergibt sich ein y-Wert von 10:
f(x) = 2,5·x = x
f(4) = 2,5·4 = 10
Dies ist wiederum der Punkt P(4|10), den wir ins Koordinatensystem einzeichnen können.
Die Funktionsgleichung lässt sich für unsere Wertetabelle (für y) wie folgt eintragen:
| x | f(x) = 2,5·x | = y |
|---|---|---|
| -3 | f(-3) = 2,5·(-3) | = -7,5 |
| -2 | f(-2) = 2,5·(-2) | = -5 |
| -1 | f(-1) = 2,5·(-1) | = -2,5 |
| 0 | f(0) = 2,5·(0) | = 0 |
| 1 | f(1) = 2,5·(1) | = 2,5 |
| 2 | f(2) = 2,5·(2) | = 5 |
| 3 | f(3) = 2,5·(3) | = 7,5 |
Übrigens ist es egal, ob die Wertetabelle horizontal oder vertikal dargestellt wird.
Im Fall einer linearen Funktionen ist dies (x|y), ein y-Wert wird einem x-Wert zugeordnet. Dies können wir dann als Punkt in ein Koordinatensystem einzeichnen.
Definitionsmenge und Wertebereich
Die Menge aller x-Elemente nennen wir Definitionsmenge.
Die Menge aller y-Elmente nennen wir Wertebereich.
Eindeutigkeit von Funktionen
Ein besonderes Merkmal von Funktionen (Zuordnungen) sei abschließend erwähnt:
Für jede Zuordnung gilt: Ein Wert aus der „Ursprungsmenge“ muss genau einen Wert zugeordnet bekommen und nicht mehrere. Jedes x zeigt auf nur ein y.
Ein x-Wert darf nur mit einem y-Wert verknüpft sein, aber nicht mit mehreren y-Werten.
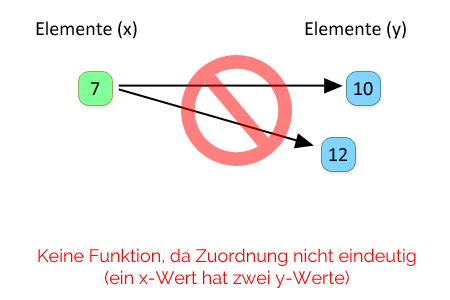
Jedoch dürfen mehrere x-Werte auf einen y-Wert zeigen.
Man nennt daher die eindeutige Zuordnung von links (x-Elemente) nach rechts (y-Elemente) „rechtseindeutig“.
