Wissen: Monotonie bei Funktionen

Begriff „Monotonie“

Das Wort „monoton“ kommt von „monotonia“ (altgriechisch), wobei mono = ein, allein und tonia = Ton. Gemeint ist damit eintönig, ohne Veränderung.

Monotonie bei Zahlenfolgen

Eine streng monoton steigende Zahlenfolge ist: 2, 3, 5, 8, 10, 20
Es gilt, dass jedes Folgeglied größer ist als das vorige: 2 < 3 < 5 < 8 < 10 < 20

Eine monoton steigende Zahlenfolge ist: 3, 5, 5, 5, 20, 110
Es gilt, dass jedes Folgeglied größer gleich dem vorigen ist: 3 < 5 = 5 = 5 < 20 < 110

Eine streng monoton fallende Zahlenfolge ist: 20, 10, 8, 5, 3, 2
Es gilt, dass jedes Folgeglied kleiner ist als das vorige: 20 > 10 > 8 > 5 > 3 > 2

Eine monoton fallende Zahlenfolge ist: 110, 20, 5, 5, 5, 3
Es gilt, dass jedes Folgeglied kleiner gleich dem vorigen ist: 110 > 20 > 5 = 5 = 5 > 3

Monotonie bei Funktionen

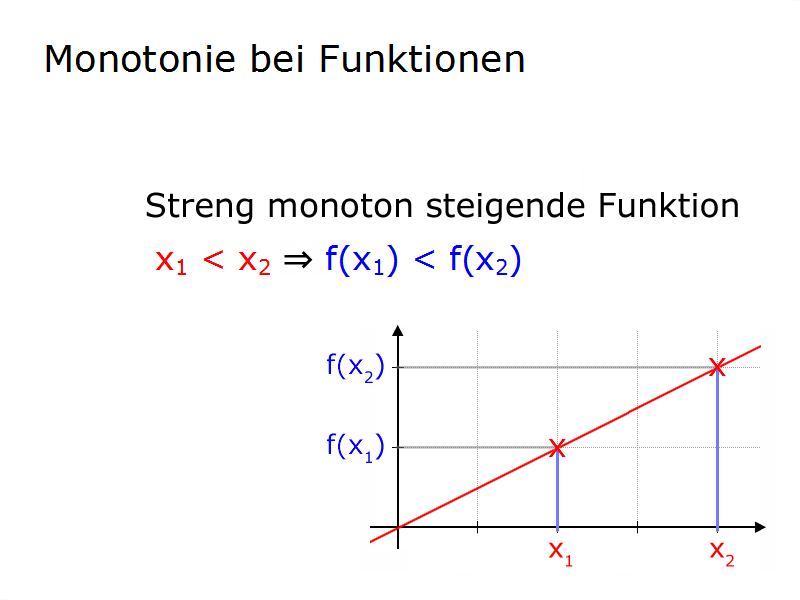
Die Formel für die streng steigende Monotonie lautet:

x₁ < x₂ ⇒ f(x₁) < f(x₂)

Das heißt, bei zunehmenden x-Werten ist jeder y-Wert bzw. Folgewert stets größer als der vorhergehenden y-Wert.

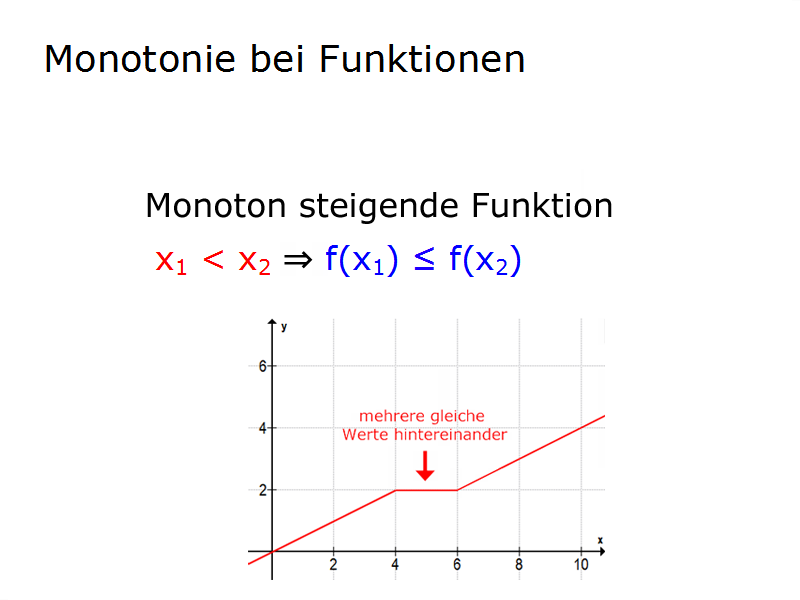
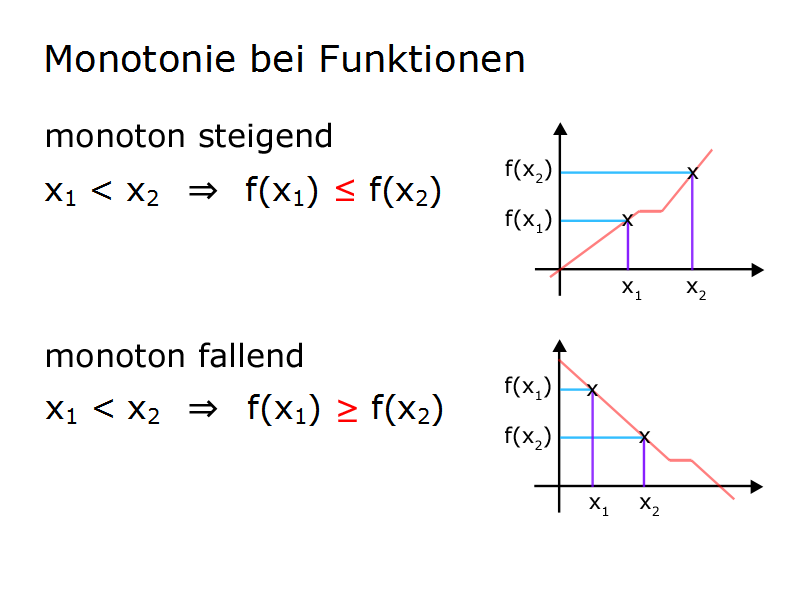
Die Formel für die steigende Monotonie lautet:

x₁ < x₂ ⇒ f(x₁) ≤ f(x₂)

Das heißt, bei zunehmenden x-Werten ist jeder y-Wert stets größer oder gleich dem vorhergehenden y-Wert.

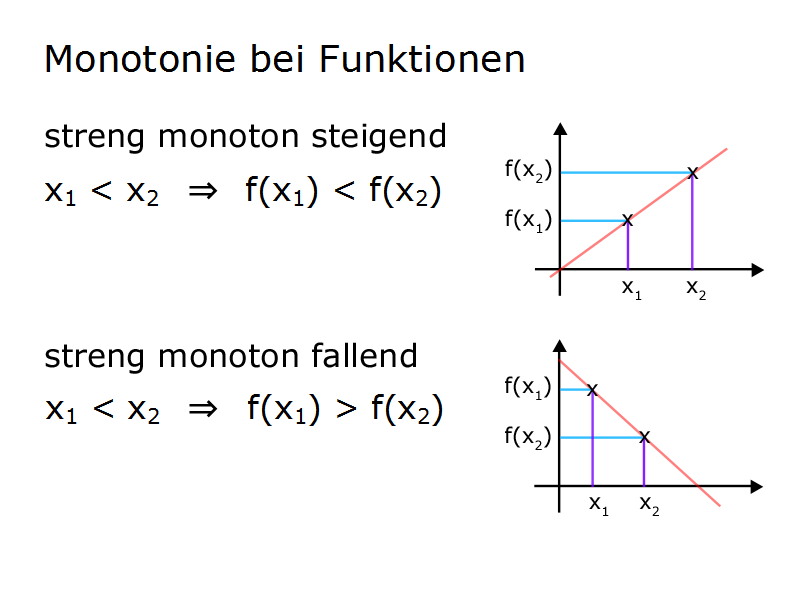
Die Formel für die streng fallende Monotonie lautet:

x₁ < x₂ ⇒ f(x₁) > f(x₂)

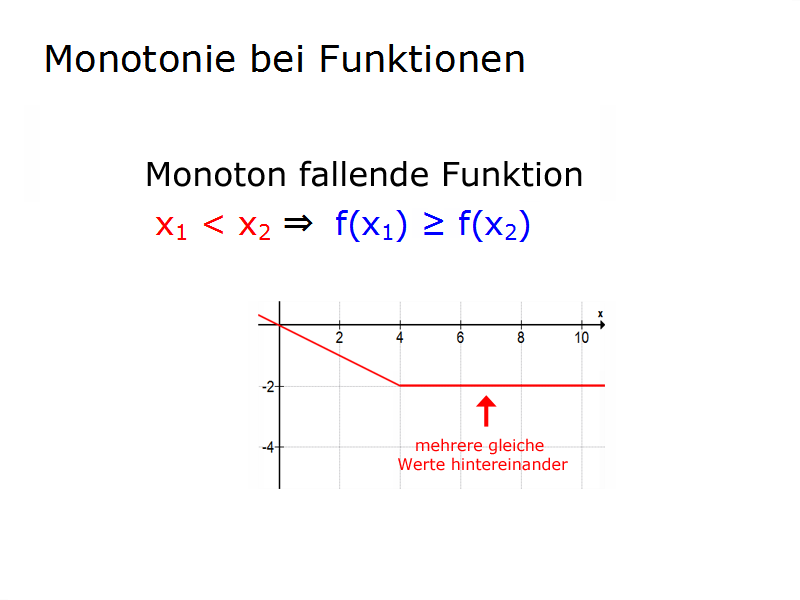
Die Formel für die fallende Monotonie lautet:

x₁ < x₂ ⇒ f(x₁) ≥ f(x₂)

Monotonie mit Darstellung der Funktionsgraphen

Monotonieverhalten richtig notieren

Intervallschreibweise:

Die Funktion f(x) = -x³ ist streng monoton fallend für ]-∞;∞[

Mengenschreibweise:
Die Funktion ist streng monoton fallend für alle x ∈ ℝ

Weiteres Beispiel

Intervallschreibweise:
Die Funktion ist streng monoton fallend für ]-∞;2]
und streng monoton steigend für [2;∞[

Mengenschreibweise:
Die Funktion ist streng monoton fallend für alle { x ∈ ℝ | x ≤ 2 }
und streng monoton steigend für alle { x ∈ ℝ | x ≥ 2 }

Abschnittsweise Funktionen

Abschnittsweise Funktionen werden wie folgt definiert und notiert, Beispiel:

Monotonieverhalten für den gesamten Graphen bestimmen:
Die Funktion ist monoton steigend für ]-∞;∞[

Monotonieverhalten für die einzelnen Abschnitte bestimmen:
f_I(x) = -x² → Die Funktion ist monoton steigend für ]-∞;-2[
f_II(x) = -4 → Die Funktion ist monoton steigend für [-2; 2]
f_III(x) = x²-8 → Die Funktion ist monoton steigend für ]2;∞[

Hier ist darauf zu achten, dass wir die -2 nicht in die Monotonie des ersten Abschnitts einschließen dürfen, weil x = -2 nicht in der Defintionsmenge dieses Abschnitts enthalten ist. Mit anderen Wort, x = -2 ist nicht Teil des 1. Abschnitts, sondern nur Teil des 2. Abschnitts.

Sonderfall bei konstanter Funktion und konstantem Funktionsabschnitt: Bei einer konstanten Funktion tritt der gleiche y-Wert hintereinander auf. Zum Beispiel für f(x)=4 haben wir die y-Werte 4, 4, 4, ... Für diesen Fall gilt die Definition der steigenden Monotonie, aber auch die der fallenden Montonie. Daher müssen wir sagen: Die konstante Funktion ist monoton steigend und monoton fallend.