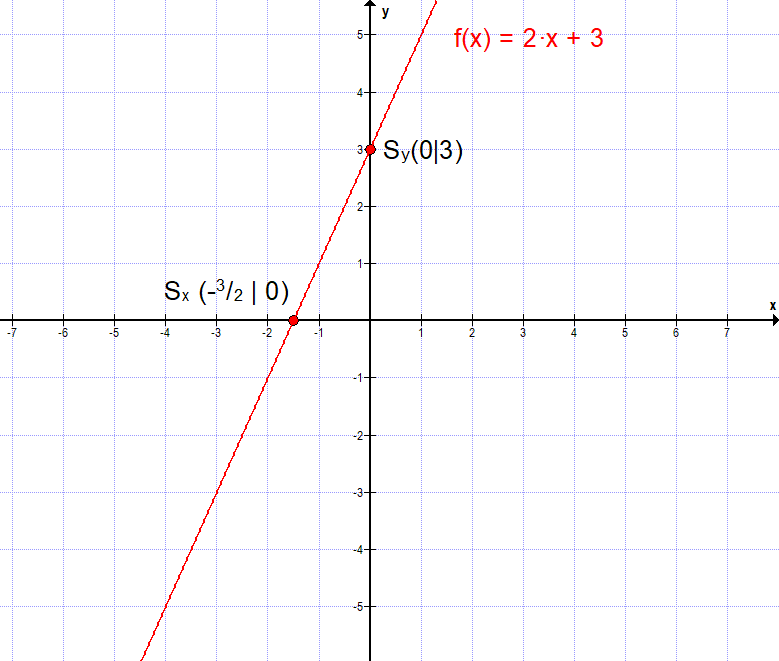Eine Aufgabenstellung bezüglich linearer Funktionen mag lauten, dass die Nullstelle (Schnittpunkt mit der Achse) bestimmt werden sollen.
Um den Schnittpunkt mit der x-Achse (die sogenannte „Nullstelle“) zu bestimmen, muss der y-Wert 0 sein. Denn ein Punkt, der auf der x-Achse liegt, hat die y-Koordinate 0 (also die Höhe 0).
Erinnern wir uns: Die x-Achse verläuft stets in der Höhe y = 0 und alle Punkte auf ihr haben ebenso die Höhe 0.
Es muss also f(x) = m·x + n = 0 bestimmt werden, um den Punkt S(x|0) zu erhalten. Dabei ist die x-Koordinate dieses Punktes die Nullstelle.
Das heißt, wir wissen, dass Punkt S(x|y) mit y = 0, also S(x|0) die Nullstelle x enthält. Rechnen wir dies allgemein aus, führt dies zu einer allgemeinen Berechnungsformel:
f(x) = m·x + n = y
f(x) = m·x + n = 0
m·x + n = 0 |-n
m·x = -n | :m
x = -n:m
\( x = -\frac{n}{m} \)
Der Schnittpunkt einer linearen Funktion kann also mit \( S_x (-\frac{n}{m}|0) \) angegeben werden.
Berechnung am Beispiel: „Bestimme die Nullstelle von f(x) = 2·x + 3.“
Der lange Rechenweg, indem wir y = 0 setzen:
f(x) = 2·x + 3 = y | y = 0
f(x) = 2·x + 3 = 0
2·x + 3 = 0 |-3
2·x = -3 |:2
x = -3:2
\( x = -\frac{3}{2} \)
Oder der kurze Rechenweg, indem wir die Berechnungsformel \( x = -\frac{n}{m} \) verwenden.
\( f(x) = 2·x + 3 = y \\ x = -\frac{n}{m} \\ x = -\frac{3}{2} \)
Beide Berechnungen führen zum gleichen Ergebnis, dem Schnittpunkt \( S_x (-\frac{3}{2}|0) \). Es ist letztlich die gleiche Berechnung.
Darstellung der Funktion als Graph: