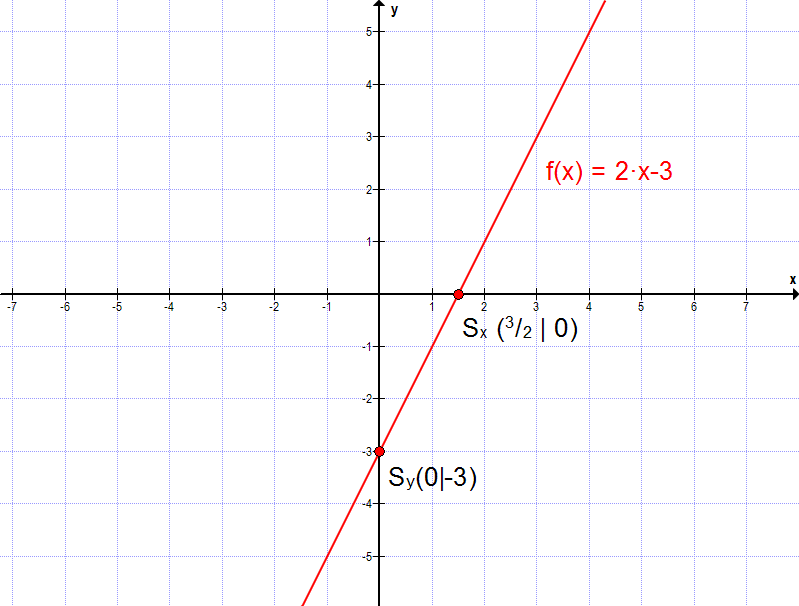Eine Aufgabenstellung bezüglich linearer Funktionen mag lauten, dass der Schnittpunkt mit der y-Achse (man sagt „y-Achsenabschnitt“) bestimmt werden soll.
Der Schnittpunkt mit der y-Achse ist schnell bestimmt. Dieser wird durch den y-Achsenabschnitt direkt angegeben.
Das heißt für f(x) = m·x + n haben wir direkt den Schnittpunkt mit Sy(0|n) bestimmt.Das kann man auch schnell zeigen, denn der Schnittpunkt mit der y-Achse verlangt, dass wir die lineare Funktion für x = 0 anschauen, das heißt der Punkt muss auf jeden Fall den x-Wert 0 haben, um auf der y-Achse zu liegen.
Und richtig, die y-Achse verläuft durch x = 0. Wir setzen also für x die 0 ein:
f(0) = m·0 + n = n
Nur n bleibt übrig und damit ist unser Schnittpunkt Sy(0|n).