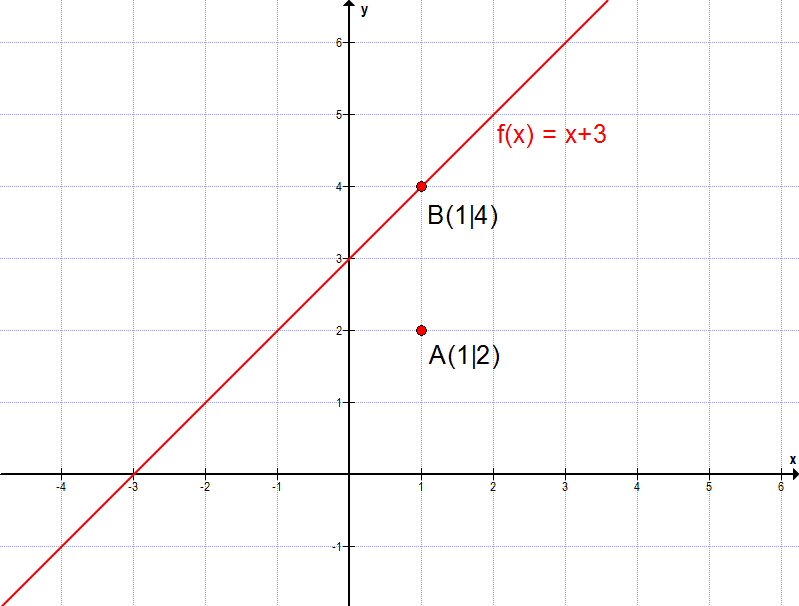Es kann vorkommen, dass von uns gefordert wird zu prüfen, ob ein bestimmter Punkt auf der Geraden einer linearen Funktion liegt. Dies wird „Punktprobe“ genannt.
Eine Möglichkeit, die Punktprobe durchzuführen, ist es, den x-Wert des Punktes P(x|y) in die lineare Funktion einzusetzen und den y-Wert zu überprüfen. Beispielhaft sieht das so aus:
„Überprüfe ob A(1|2) oder B(1|4) auf der linearen Funktion mit f(x) = x + 3 liegt.“
Herangehensweise:
1. Funktion aufstellen:
f(x) = x + 3
2. x-Wert des zu überprüfenden Punktes einsetzen und berechnen. Bei den Punkten A und B ist dies x = 1:
f(x) = x + 3 | x = 1
f(1) = 1 + 3 = 4
Man nimmt sich den x-Wert 1 und setzt ihn in die Funktionsgleichung ein. Der errechnete Wert ist der y-Wert. Dieser wird nun mit dem y-Wert des zu prüfenden Punktes verglichen.
In diesem Falle haben wir y = 4 erhalten, was dem y-Wert von Punkt B mit B(1|4) entspricht. Folglich liegt Punkt B auf der Geraden, wohingegen A abseits der Geraden liegt.