Kurs: Trigonometrie
Dieser Kurs führt in das Thema „Trigonometrie“ ein. Wir lernen, wie die Trigonometrie entstanden ist, was Sinus/Kosinus/Tangens sind und welche Vorteile sie bei der Dreiecksberechnung bringen.
-
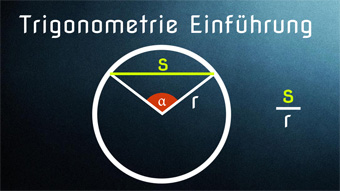 TRI01: Einführung zur Trigonometrie Dieses Mathe-Video bietet eine Einführung in die Trigonometrie. Wir klären den Begriff, blicken in die Geschichte der Trigonometrie und zeigen einige Anwendungen. Auch lernen wir, was eine Sehnenfunktion ist.▷ Inhalte verstanden?
TRI01: Einführung zur Trigonometrie Dieses Mathe-Video bietet eine Einführung in die Trigonometrie. Wir klären den Begriff, blicken in die Geschichte der Trigonometrie und zeigen einige Anwendungen. Auch lernen wir, was eine Sehnenfunktion ist.▷ Inhalte verstanden? -
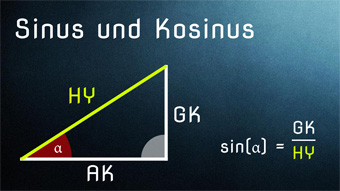 TRI02: Sinus und Kosinus In diesen Mathe-Videos wird einfach erklärt, was Sinus und Kosinus sind und wie sie funktionieren. Wir lernen, wie sie die Berechnung von Dreiecken vereinfachen.▷ Inhalte verstanden?
TRI02: Sinus und Kosinus In diesen Mathe-Videos wird einfach erklärt, was Sinus und Kosinus sind und wie sie funktionieren. Wir lernen, wie sie die Berechnung von Dreiecken vereinfachen.▷ Inhalte verstanden? -
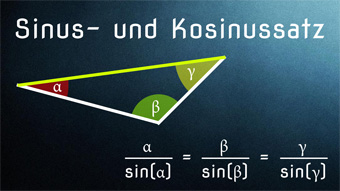 TRI03: Sinussatz und Kosinussatz In diesen Mathe-Videos lernen wir, wie Sinus und Kosinus zur Berechnung von allgemeinen Dreiecken benutzt werden. Hier treffen wir auf den Sinussatz und den Kosinussatz. Auch lernen wir (Ko)Sinuswerte bis 180 Grad kennen!▷ Inhalte verstanden?
TRI03: Sinussatz und Kosinussatz In diesen Mathe-Videos lernen wir, wie Sinus und Kosinus zur Berechnung von allgemeinen Dreiecken benutzt werden. Hier treffen wir auf den Sinussatz und den Kosinussatz. Auch lernen wir (Ko)Sinuswerte bis 180 Grad kennen!▷ Inhalte verstanden? -
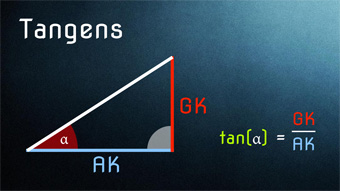 TRI04: Tangens Wir lernen: Was ist der Tangens? Wie wird Tangens definiert und angewendet (z. B. um Steigungen von linearen Funktionen zu bestimmen). Wir klären, wie man mit dem Arkustangens einfach vom Tangenswert zum Winkel kommt.▷ Inhalte verstanden?
TRI04: Tangens Wir lernen: Was ist der Tangens? Wie wird Tangens definiert und angewendet (z. B. um Steigungen von linearen Funktionen zu bestimmen). Wir klären, wie man mit dem Arkustangens einfach vom Tangenswert zum Winkel kommt.▷ Inhalte verstanden? -
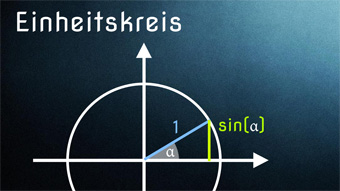 TRI05: Einheitskreis In diesen Mathe-Videos wird der Einheitskreis einfach erklärt. Wir lernen Sinus, Kosinus und Tangens am Einheitskreis kennen. Zusätzlich schauen wir Identitäten und den trigonometrischen Pythagoras an.▷ Inhalte verstanden?
TRI05: Einheitskreis In diesen Mathe-Videos wird der Einheitskreis einfach erklärt. Wir lernen Sinus, Kosinus und Tangens am Einheitskreis kennen. Zusätzlich schauen wir Identitäten und den trigonometrischen Pythagoras an.▷ Inhalte verstanden? -
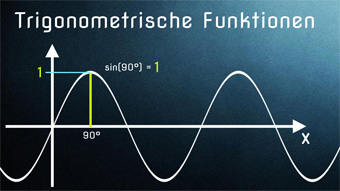 TRI06: Trigonometrische Funktionen Die Videos erklären einfach, wie die Sinusfunktion entsteht und was die Sinusschwingung bedeutet. Nach der Einführung sehen wir uns die Kosinusfunktion und die Tangensfunktion an.▷ Inhalte verstanden?
TRI06: Trigonometrische Funktionen Die Videos erklären einfach, wie die Sinusfunktion entsteht und was die Sinusschwingung bedeutet. Nach der Einführung sehen wir uns die Kosinusfunktion und die Tangensfunktion an.▷ Inhalte verstanden? -
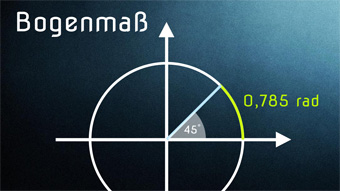 TRI07: Bogenmaß und Kreiszahl Pi In diesen Videos erklären wir, was Bogenmaß und Radiant sind, wie die Kreiszahl Pi entsteht und wie wir von Grad zu Bogenmaß kommen, auch mit dem Taschenrechner.▷ Inhalte verstanden?
TRI07: Bogenmaß und Kreiszahl Pi In diesen Videos erklären wir, was Bogenmaß und Radiant sind, wie die Kreiszahl Pi entsteht und wie wir von Grad zu Bogenmaß kommen, auch mit dem Taschenrechner.▷ Inhalte verstanden? -
 TRI08: Trigonometrische Gleichungen In dieser Mathe-Lektion erklären wir, wie ihr trigonometrische Gleichungen einfach lösen könnt. Auch lernen wir Periode und Periodizitätssummand kennen.▷ Inhalte verstanden?
TRI08: Trigonometrische Gleichungen In dieser Mathe-Lektion erklären wir, wie ihr trigonometrische Gleichungen einfach lösen könnt. Auch lernen wir Periode und Periodizitätssummand kennen.▷ Inhalte verstanden? -
 TRI09: Additionstheoreme Mit erstklassigen Mathe-Videos werden hier die Additionstheoreme für Sinus, Kosinus und Tangens einfach und vollständig erklärt. Zusätzlich lernen wir die Doppelwinkelfunktionen kennen.▷ Inhalte verstanden?
TRI09: Additionstheoreme Mit erstklassigen Mathe-Videos werden hier die Additionstheoreme für Sinus, Kosinus und Tangens einfach und vollständig erklärt. Zusätzlich lernen wir die Doppelwinkelfunktionen kennen.▷ Inhalte verstanden? -
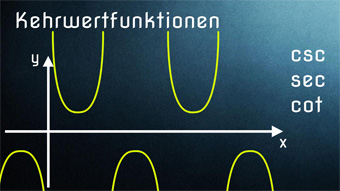 TRI10: Kehrwertfunktionen (Trigonometrie) Hier lernt ihr die Kehrwertfunktionen Sekans, Kosekans und Kotangens kennen. Testet euer Wissen mit den Lernprogrammen oder kauft euch die Videos zur Lektion.▷ Inhalte verstanden?
TRI10: Kehrwertfunktionen (Trigonometrie) Hier lernt ihr die Kehrwertfunktionen Sekans, Kosekans und Kotangens kennen. Testet euer Wissen mit den Lernprogrammen oder kauft euch die Videos zur Lektion.▷ Inhalte verstanden?
