Lektion VEK01: Einführung zu Vektoren
Dies ist die erste Lektion zu den Vektoren. Hier lernen wir, was hinter dem Begriff „Vektor“ steckt, wozu man Vektoren benutzen kann und wie sie uns beim Rechnen helfen.
Für Vektoren in der Ebene gibt es mehrere Definitionen. Die geometrische Definition lautet: Ein Vektor ist eine gerichtete Strecke. Die algebraische ("rechnerische") Definition lautet: Ein Vektor ist ein Zahlenpaar. Erfahrt hierzu mehr in den Videos.
Einführung Vektoren - Geom. Verschiebung berechnen
Was bedeutet Vektor, geometrische Verschiebung in der Ebene mit Vektoren exakt berechnen, Komponenten des Vektors, Vektor als Pfeile mit bestimmter Länge und bestimmter Richtung, Vektornotation, Repräsentanten des Vektors.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
VEK01-2 Einführung Vektoren - Definition und AnwendungsbeispieleWas ist ein Vektor? Definition geometrisch und als Zahlenpaar. Schreibweisen für Vektoren. Geschwindigkeit als Anwendungsbeispiele für Vektoren: Gleichförmige Bewegung, kreisförmige Bewegung, Bewegung mit Verzögerung. Übungen zur Gleichheit von Vektoren.
Im Folgenden findet ihr einige Programme, mit denen ihr das neue Wissen zu Vektoren testen könnt.
-
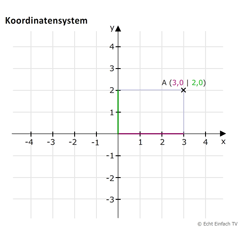 Koordinatensystem (Linien 2)In diesem Koordinatensystem bewegt ihr einen Punkt, dessen Koordinaten P(x|y) angezeigt werden. Die Linien helfen euch beim Ablesen.
Koordinatensystem (Linien 2)In diesem Koordinatensystem bewegt ihr einen Punkt, dessen Koordinaten P(x|y) angezeigt werden. Die Linien helfen euch beim Ablesen. -
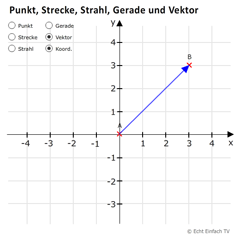 Punkt, Strecke, Strahl, Gerade, VektorHier könnt ihr euch testen, ob ihr den Unterschied zwischen Punkt, Strecke, Strahl, Gerade und Vektor erkennt.
Punkt, Strecke, Strahl, Gerade, VektorHier könnt ihr euch testen, ob ihr den Unterschied zwischen Punkt, Strecke, Strahl, Gerade und Vektor erkennt. -
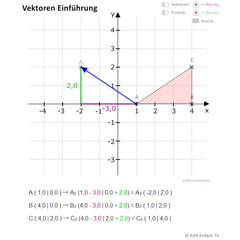 Vektoren EinführungDieses Programm ist eine Einführung in die Vektoren. Eine geometrische Verschiebung wird durch Vektoren (Zahlenpaare) exakt berechenbar gemacht.
Vektoren EinführungDieses Programm ist eine Einführung in die Vektoren. Eine geometrische Verschiebung wird durch Vektoren (Zahlenpaare) exakt berechenbar gemacht. -
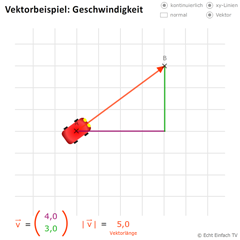 Vektorbeispiel Geschwindigkeit 1Vektoren helfen uns, Geschwindigkeiten zu beschreiben. Mit diesem Programm könnt ihr ein Auto eine gleichförmige Bewegung ausführen lassen.
Vektorbeispiel Geschwindigkeit 1Vektoren helfen uns, Geschwindigkeiten zu beschreiben. Mit diesem Programm könnt ihr ein Auto eine gleichförmige Bewegung ausführen lassen. -
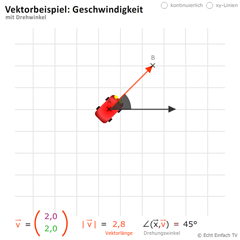 Vektorbeispiel Geschwindigkeit 2Vektoren helfen uns, Geschwindigkeiten zu beschreiben. Mit diesem Programm könnt ihr ein Auto eine kreisförmige Bewegung ausführen lassen.
Vektorbeispiel Geschwindigkeit 2Vektoren helfen uns, Geschwindigkeiten zu beschreiben. Mit diesem Programm könnt ihr ein Auto eine kreisförmige Bewegung ausführen lassen. -
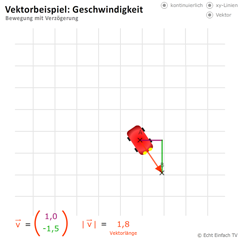 Vektorbeispiel Geschwindigkeit 3Vektoren helfen uns, Geschwindigkeiten zu beschreiben. Mit diesem Programm könnt ihr ein Auto eine verzögerte Bewegung ausführen lassen.
Vektorbeispiel Geschwindigkeit 3Vektoren helfen uns, Geschwindigkeiten zu beschreiben. Mit diesem Programm könnt ihr ein Auto eine verzögerte Bewegung ausführen lassen.
Hier findest du 2 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 2 Lernchecks, mit denen du dein Wissen testen kannst.
Häufige Fragen:
Finde weitere Fragen und Antworten in der Mathelounge.