Additionstheorem Kosinus

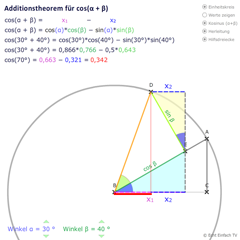
Herleitung des Additionstheorems für Kosinus

Wir wollen klären, welches Additionstheorem für Kosinus mit cos(α + β) gilt. Nehmen wir uns zuerst eine Grafik vom Einheitskreis und zeichnen beide Winkel mit Dreiecken ein:

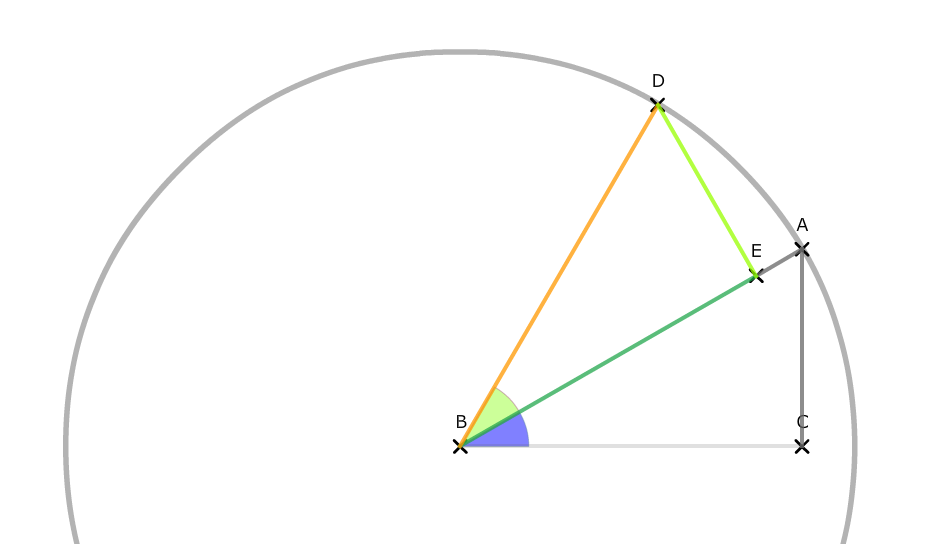
Zeichnen wir nun Hilfslinien ein, durch die zwei neue Dreiecke entstehen:

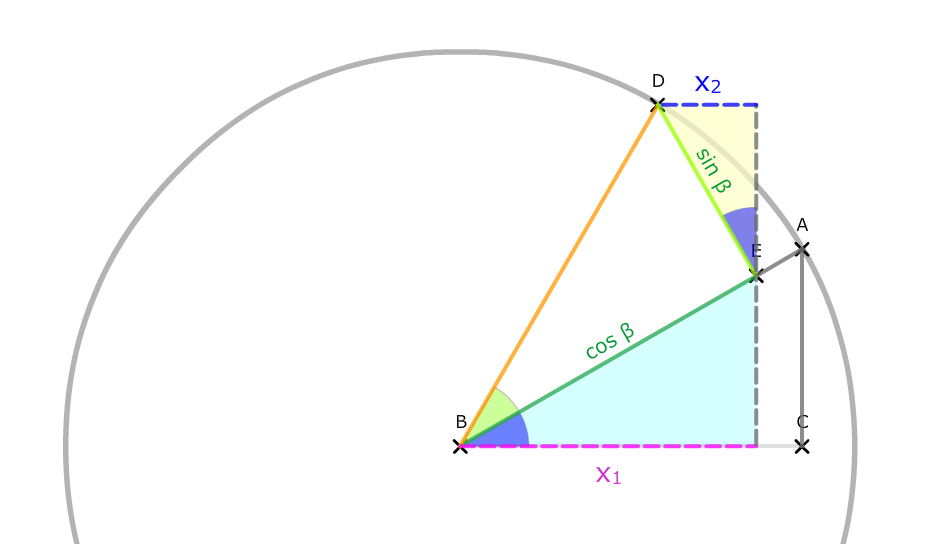
Wir sehen, dass sich der Kosinus vom Gesamtwinkel, also cos(α+β), ergibt aus x₁ - x₂.

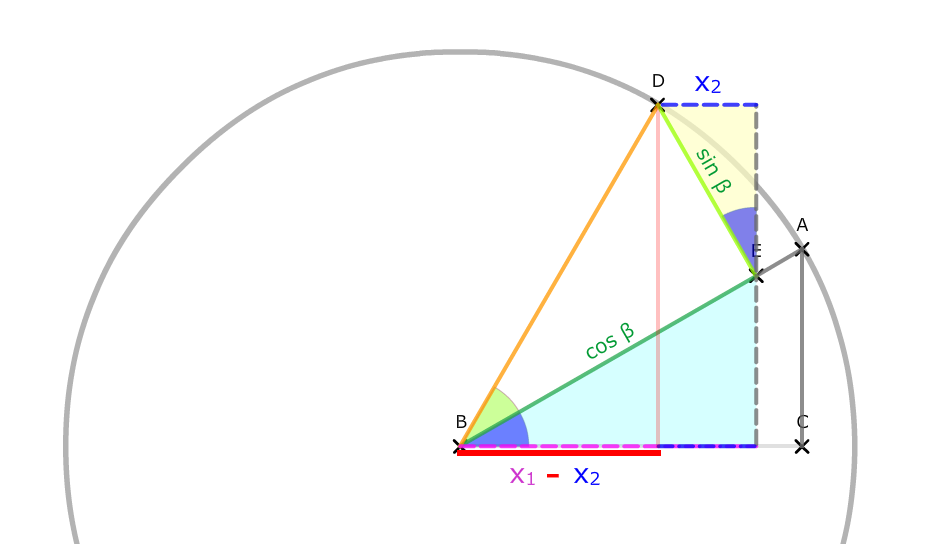
Wir müssen also berechnen: cos(α+β) = x₁ - x₂.

Die Strecke x₁ erhalten wir mit:

cos(α) = Ankathete / Hypotenuse

cos(α) = x₁ / cos(β)   | ·cos(β)

x₁ = cos(α) · cos(β)

Die Strecke x₂ erhalten wir mit:

sin(α) = Gegenkathete / Hypotenuse

sin(α) = x₂ / sin(β)

x₂ = sin(α) · sin(β)

Damit können wir also das Additionstheorem für Kosinus aufstellen:

cos(α + β) = x₁ - x₂

cos(α + β) = cos(α) · cos(β) - sin(α) · sin(β)

Auf diese Art und Weise können wir die Kosinuswerte beliebiger Winkel bestimmen, die sich aus zwei Winkeln ergeben.

Additionstheorem für cos(α - β)

Bei der Herleitung dieses Kosinus-Additionstheorems gehen wir genauso vor wie zuvor. Wir setzen zuerst (-β) ein:

cos(α + β) = cos(α) · cos(β) - sin(α) · sin(β)

cos(α + (-β)) = cos(α) · cos(-β) - sin(α) · sin(-β)

Nun müssen wir die negativen Vorzeichen bei -β wegbekommen. Nutzen wir die Identität cos(x) = cos(-x):

cos(α + (-β)) = cos(α) · cos(-β) - sin(α) · sin(-β)

cos(α + (-β)) = cos(α) · cos(β) - sin(α) · sin(-β)

Und als nächstes sin(x) = -sin(-x), damit:

cos(α + (-β)) = cos(α) · cos(β) - sin(α) · (-sin(β))

Das negative Vorzeichen brücksichtigt in der Addition bzw. Subtraktion und wir erhalten:

cos(α - β) = cos(α) · cos(β) + sin(α) · sin(β)

Jetzt können wir die beiden Additionstheoreme für Kosinus zusammenfassen:

1. cos(α + β) = cos(α) · cos(β) - sin(α) · sin(β)

2. cos(α - β) = cos(α) · cos(β) + sin(α) · sin(β)

Zusammengefasst mit Plus-Minus:

cos(α ± β) = cos(α) · cos(β) ± sin(α) · sin(β)