Additionstheorem Sinus

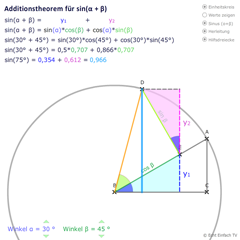
Einführung

Bei den sogenannten „Additionstheoremen“ wollen wir den Sinuswert (oder Kosinuswert oder Tangenswert) aus der Summe von zwei Winkeln berechnen.

Wir fragen uns, was ergibt:

sin(α + β) = ?
cos(α + β) = ?
tan(α + β) = ?

Herleitung des Additionstheorems für Sinus

Vorüberlegung zum Addieren von Sinuswerten

Schauen wir, welche Lösungsformel wir ermitteln können für:

sin(α + β) = ?

Wir dürfen nicht einfach den Sinus von beiden Winkeln einzeln ziehen und addieren, da das nicht der gleiche Wert wäre. Als Beispiel:

sin(30° + 60°) = sin(90°) = 1

sin(30°) + sin(60°) ≈ 0,5 + 0,866 = 1,366

sin(30°) + sin(60°) ≠ sin(30° + 60°)

Um den Sinuswert zu bestimmen, der sich aus zwei Teilwinkeln ergibt, benötigen wir die Additionstheoreme, denn sie geben uns eine Berechnungsvorschrift, um direkt eine Lösung aus sin(30° + 60°) zu ermitteln.

Wiederholung Einheitskreis

Werfen wir einen Blick auf den Einheitskreis und wiederholen: Er hat bekanntlich einen Radius von 1, die Hypotenuse des Hilfsdreiecks ist damit immer 1 lang.

sin(α) = Gegenkathete / Hypotenuse   | Hypotenuse = 1
sin(α) = Gegenkathete / 1
sin(α) = Gegenkathete

Direkt an der Gegenkathete können wir also den Sinuswert ablesen. Gleiches gilt für den Kosinus (Ankathete). Und genau dieses Wissen hilft uns bei den Additionstheoremen weiter.

Herleitung der Lösungsformel

Die Addition der zwei Winkel können wir so visualisieren:

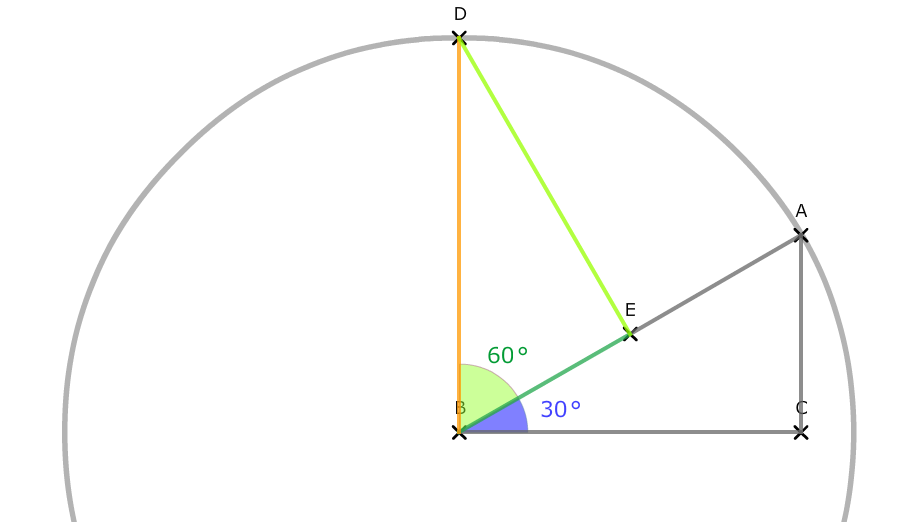
Wir gehen schrittweise vor, um eine allgemeine Lösungsformel zu finden. Hierzu zeichnen wir zuerst von Punkt D aus eine Senkrechte auf die Hypotenuse BA, Punkt E entsteht:

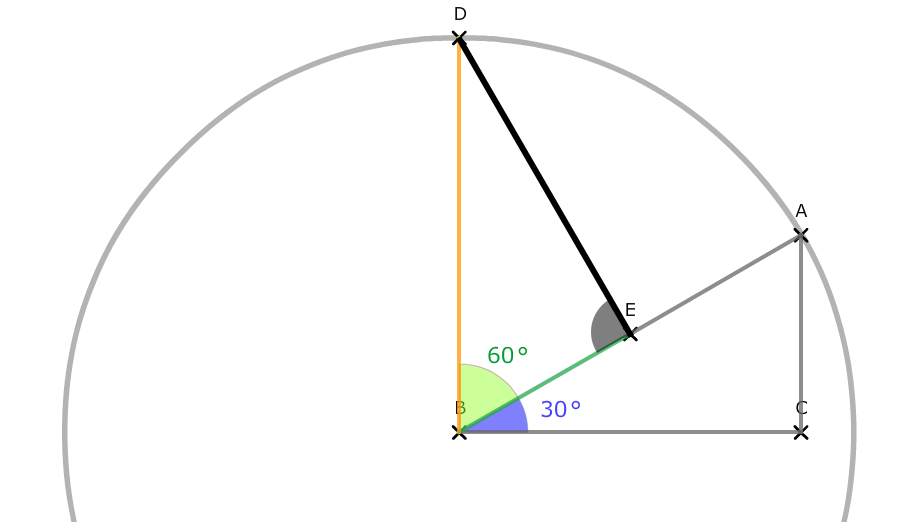
Wir erkennen, dass ein rechtwinkliges Dreieck DBE entsteht, es ist das Referenzdreieck für Winkel β.

Jetzt zeichnen wir durch den neuen Punkt E eine Senkrechte nach unten, die uns den sin(α + β) anzeigt. Mit dieser neuen Linie erhalten wir zwei neue Dreiecke:

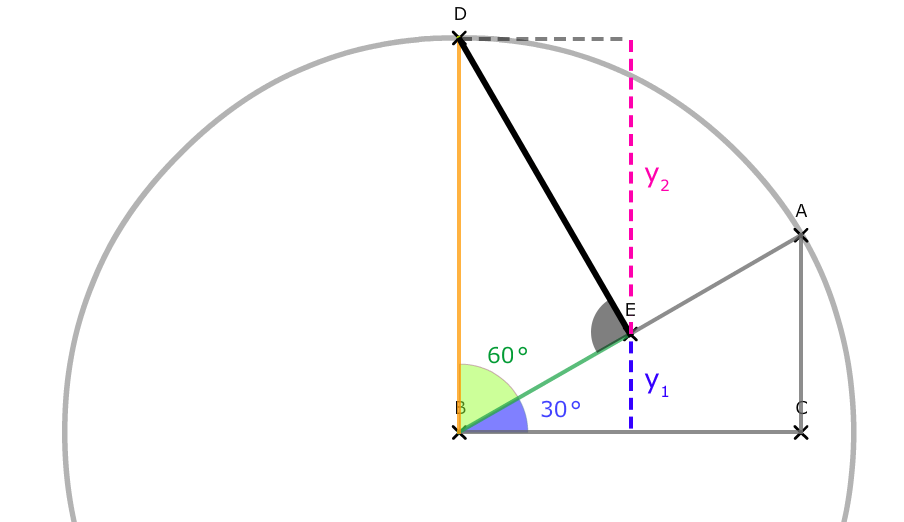
Wir sehen nun:

Strecke y₁ + Strecke y₂ = sin(α + β)

Wir müssen nur eine Möglichkeit finden, y₁ und y₂ zu berechnen, denn damit hätten wir den Sinuswert des Gesamtwinkels.

Zudem erkennen wir, dass die Seiten des Dreiecks mit Winkel β nun auch mit sin und cos ausgedrückt werden können, denn die Hypotenuse ist 1 lang: Die Ankathete ist cos(β) und die Gegenkathete ist sin(β).

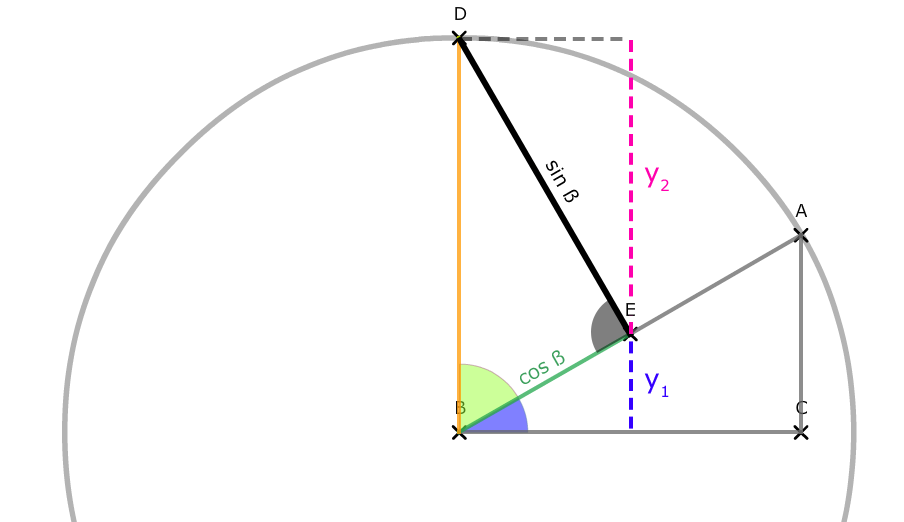
Berechnung von Strecke y₁

Berechnen wir y₁ mit Hilfe des kleinen hellblauen Dreiecks: Dort ist y₁ die Gegenkathete von a. Zudem ist cos(β) die Länge der Hypotenuse des kleinen Dreiecks.

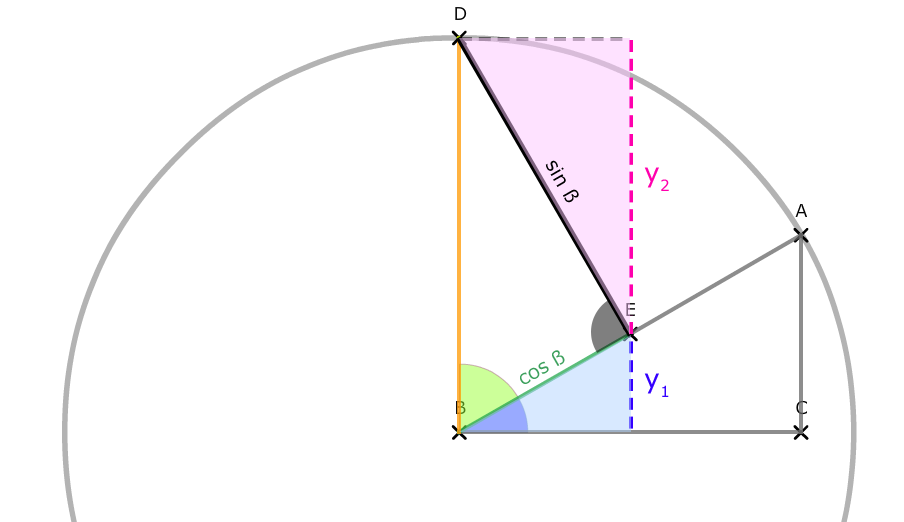
Wir können nun mit Blick auf das kleine blaue Dreieck aufstellen:

sin(α) = Gegenkathete / Hypotenuse
sin(α) = y₁ / cos(β)   | ·cos(β)
y₁ = sin(α) · cos(β)

Mit sin(α) errechnen wir also einen Anteil aus der Länge cos(β), und das ist die Länge von y₁.

Berechnung von Strecke y₂

Zuerst ein Schaubild:

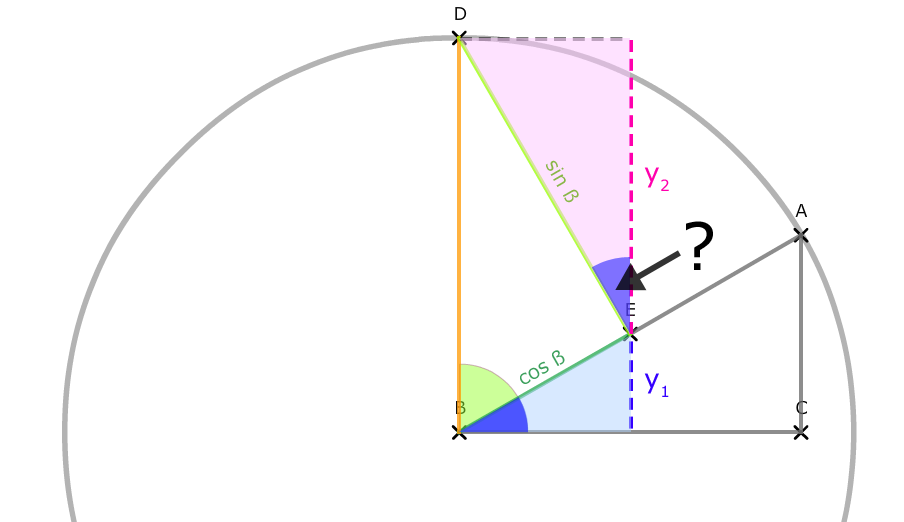
Die gesuchte Strecke y₂ ist Ankathete des rosa Dreiecks. Als erstes müssen wir die Größe des eingezeichneten Winkels kennen. Dieser Winkel ist genauso groß wie Winkel α, der Grund: Das hellblaue Dreieck und das rosa Dreieck sind rechtwinklige Dreiecke, das heißt beide besitzen einen Winkel von 90°. Die anderen Winkel ergeben sich aus: α und 90° - α, denn alle drei müssen zusammen nachher 180° ergeben. Zudem teilen sich beide Dreiecke Winkel, die mit α in Verbindung stehen:

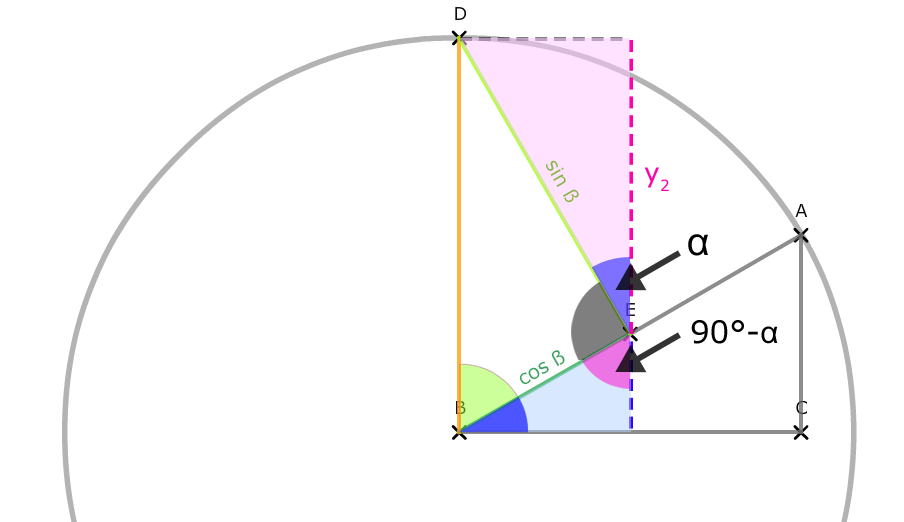
Wir erkennen, dass wenn ein Winkel α und ein weiterer 90° ist, der dritte Winkel 90° - α sein muss, was für beide Dreiecke gilt. Sie haben beide demnach die gleichen Winkelgrößen.

Jetzt können wir für das rosa Dreieck aufstellen:

cos(α) = AK / HY
cos(α) = y₂ / sin(β)   | · sin(β)
y₂ = cos(α) · sin(β)

Formel für Strecke y₁ + y₂

sin(α + β) = Strecke y₁ + Strecke y₂
sin(α + β) = sin(α) · cos(β) + cos(α) · sin(β)

In Worten: y₁ ergibt sich, in dem wir den Anteil bilden, also den sin(α) berechnen und diesen mit der Seite cos(β) multiplizieren. Und y₂ ergibt sich, indem wir den Anteil bilden, also den cos(α) aus dieser Seite, die sin(β) lang ist. Und dann können wir die beiden Terme addieren und erhalten die Gesamtlänge, die ja der Sinuswert unseres Gesamtwinkels ist, also sin(α + β).

Additionstheorem für sin(α + β)

Die zuvor gezeigte Formel nennen wir Additionstheorem, mit ihr können wir die Sinuswerte aus zwei einzelnen Winkeln zusammen berechnen:

sin(α + β) = sin(α) · cos(β) + cos(α) · sin(β)

Ein Anwendungsbeispiel:

sin(α + β) = sin(α) · cos(β) + cos(α) · sin(β)

sin(30° + 60°) = sin(30°) · cos(60°) + cos(30°) · sin(60°)
sin(30° + 60°) = 0,5 · 0,5 + 0,866 · 0,866
sin(30° + 60°) = 0,999956…
sin(30° + 60°) ≈ 1

sin(90°) = 1

Additionstheorem für sin(α - β)

Betrachten wir, wie wir verfahren müssen, wenn wir statt (α + β) ein (α - β) haben. Der Unterschied ist, dass wir in die Formel statt β ein -β eintragen, dabei bleibt die Addition erhalten und das Additionstheorem ist immer noch korrekt:

sin(α + β) = sin(α) · cos(β) + cos(α) · sin(β)
sin(α + (-β)) = sin(α) · cos(-β) + cos(α) · sin(-β)

Unser Ziel ist es, nur a und β ohne Vorzeichen zu haben.

Bei den Identitäten hatten wir gelernt, dass cos(x) = cos(-x). Damit können wir das cos(-β) als cos(β) schreiben:

sin(α + (-β)) = sin(α) · cos(-β) + cos(α) · sin(-β)
sin(α + (-β)) = sin(α) · cos(β) + cos(α) · sin(-β)

Für das sin(-β) können wir ebenfalls eine Identität verwenden und zwar: sin(x) = -sin(-x).

Damit ergibt sich:

sin(α + (-β)) = sin(α) · cos(-β) + cos(α) · sin(-β)
sin(α + (-β)) = sin(α) · cos(β) + cos(α) · (-sin(β))

Das negative Vorzeichen in der Addition berücksichtigt und wir erhalten:

sin(α - β) = sin(α) · cos(β) - cos(α) · sin(β)

Jetzt können wir die beiden Additionstheoreme für Sinus zusammenfassen:

1. sin(α + β) = sin(α) · cos(β) + cos(α) · sin(β)

2. sin(α - β) = sin(α) · cos(β) - cos(α) · sin(β)

Zusammengefasst mit Plus-Minus:

sin(α ± β) = sin(α) · cos(β) ± cos(α) · sin(β)