Unter Verwendung der Definitionsgleichung (Gl. 28) der imaginären Einheit i können die verschiedenen Potenzen von i bestimmt werden:
\( {i^0} = 1 \\ {i^1} = \left( {\sqrt[2]{ { - 1} } } \right) = i \\ {i^2} = {\left( {\sqrt[2]{ { - 1} } } \right)^2} = - 1 \\ {i^3} = {\left( {\sqrt[2]{ { - 1} } } \right)^3} = {\left( {\sqrt[2]{ { - 1} } } \right)^2} \cdot {\left( {\sqrt[2]{ { - 1} } } \right)^1} = - 1 \cdot i \\ {i^4} = {\left( {\sqrt[2]{ { - 1} } } \right)^4} = {\left( {\sqrt[2]{ { - 1} } } \right)^2} \cdot {\left( {\sqrt[2]{ { - 1} } } \right)^2} = - 1 \cdot \left( { - 1} \right) = 1 \\ {i^5} = {\left( {\sqrt[2]{ { - 1} } } \right)^5} = {\left( {\sqrt[2]{ { - 1} } } \right)^2} \cdot {\left( {\sqrt[2]{ { - 1} } } \right)^2} \cdot \left( {\sqrt[2]{ { - 1} } } \right) = 1 \cdot i \) Gl. 37
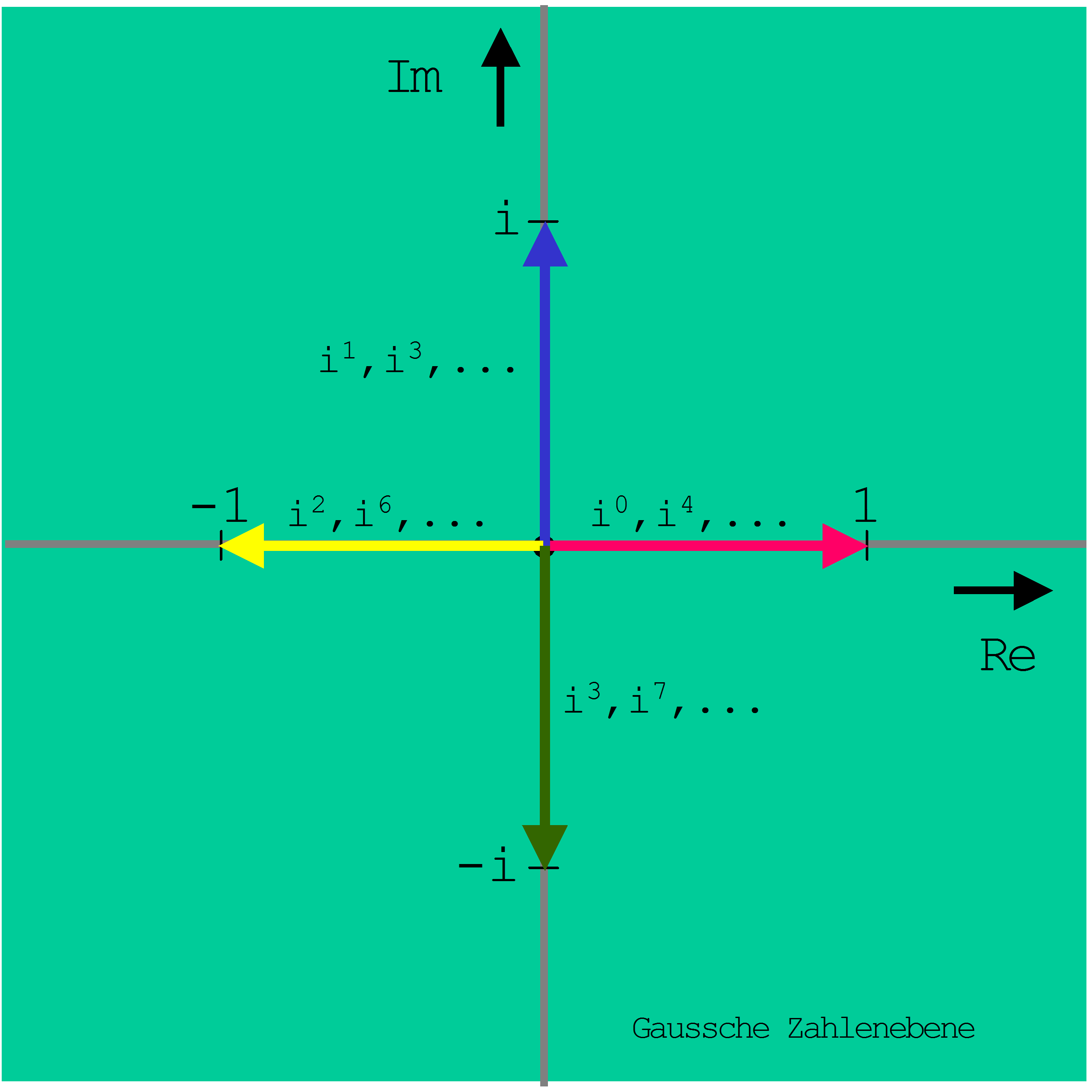
und so weiter. In der Gauss’schen Zahlenebene sieht das so aus: