Sind bei einer quartischen Gleichung b=0, d=0 und e=0, so erhalten wir folgende Form:
a·x4 + c·x2 = 0
Dieser Gleichungstyp vierten Grades lässt sich durch das Ausklammern des Faktors x2 vereinfachen:
a·x4 + c·x2 = 0
(a·x2 + c)·x2 = 0
x = 0 resultiert als doppelte Nullstelle aus x2 = 0 und das Problem reduziert sich zu:
a·x2 + c = 0
Die Begründung für diese Vereinfachung liegt darin, dass ein Produkt genau dann Null ist, wenn mindestens einer seiner Faktoren Null ist. Dieser einfache Zusammenhang wird gelegentlich als Satz vom Nullprodukt bezeichnet.
Die Lösungen zu dieser Gleichung erhält man auf ähnliche Weise wie für den Gleichungstyp a·x4 + e = 0.
Sie ergeben sich mit:
\( x_{1,2} = \sqrt{-\frac{c}{a}} \)
Wieder sieht man, dass für die Existenz weiterer Nullstellen genau einer der beiden Koeffizienten a oder c negativ sein muss.
Es sei zum Beispiel eine solche Gleichung mit -x4 + 25x2 = 0 gegeben. Dann ist die doppelte Nullstelle x1 = 0.
Die anderen beiden Nullstellen ergeben sich aus:
\( x_{2,3} = \pm \sqrt{-\left(\frac{25}{-1}\right)} = \pm 5 \)
Dies kann man zur Übung auch handschriftlich mit den beiden konkreten Koeffizienten a = -1 und c = 25 nachvollziehen.
Eine andere Möglichkeit, die Nullstellen zu nummerieren, ist die doppelte Nullstelle als zwei übereinanderfallende Nullstellen x1 = x2 = 0 aufzufassen. Die anderen beiden (nicht-trivialen) Nullstellen erhalten dann die Bezeichnung x3 und x4.
Es sei aber darauf hingewiesen, dass x1 = x2 = 0 eigentlich nur eine einzige Nullstelle ist, die aufgrund ihrer Vielfachheit (ihre Vielfachheit ist 2) zwei verschiedenen Namen x1 und x2 trägt.
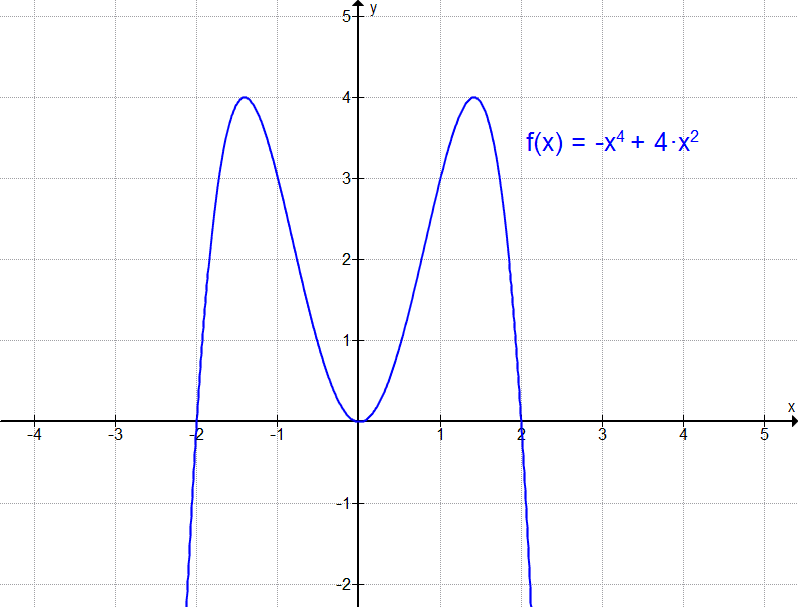
Die Nullstellen einer quartischen Funktion lassen sich aus ihrer grafischen Darstellung ablesen. Als Beispiel sei der Graph der Funktion f(x) = -x4 + 4·x2 mit doppelter Nullstelle bei x = 0 gezeigt: