Betrachten wir uns das Lösen von Gleichungen n-ten Grades (endlicher Ordnung) als Nullstellen von Polynomfunktionen.
„Endlicher Ordnung“ meint, dass der Grad der Funktion endlich sein muss, also eine Polynomfunktion.
Wird die linke Seite der quartischen Gleichung a·x4 + e = 0 als Polynomfunktion f(x) = a·x4 + e aufgefasst, so entsprechen die Lösungen der quartischen Gleichung den Nullstellen der Polynomfunktion.
Allgemein lässt sich feststellen, dass die Nullstellen einer Polynomfunktion in natürlicher Weise den Lösungen der dazugehörigen Gleichung endlicher Ordnung, und zwar f(x) = 0, entsprechen.
Hier als Beispiel ein Bild der Polynomfunktion f(x) = x4 - 5·x2 + 4 mit ihren vier Nullstellen x = -2, x = -1, x = 1, x = 2.
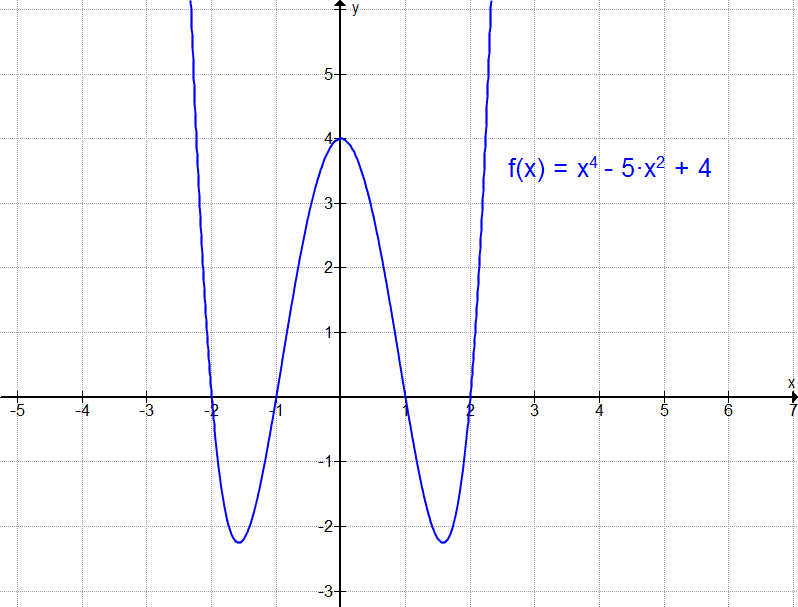
Interaktiver Graph:
~plot~ x^4 - 5*x^2 + 4; [[5]];noinput ~plot~
