Der Sinussatz ist ein Hilfsmittel, um schnell fehlende Seiten und Winkel in allgemeinen Dreiecken über Verhältnisse auszurechnen. Er spielt in der Dreiecksberechnung und der Trigonometrie eine wichtige Rolle.
Erinnern wir uns, wie der Sinus definiert ist: sin(α) = Gegenkathete / Hypothenuse = GK / HY
Wer sich nicht daran erinnert, schaut sich unbedingt den Artikel: Sinus jetzt noch mal an.
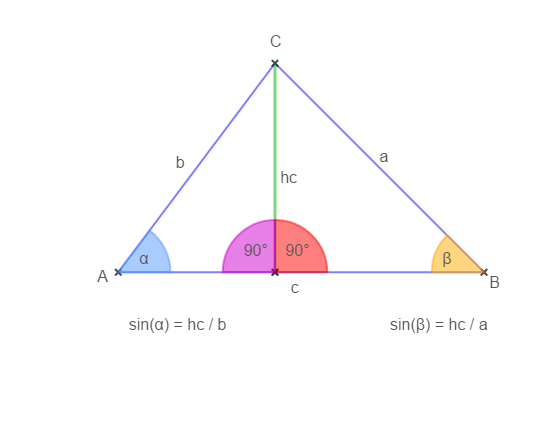
Beim Betrachten von allgemeinen Dreiecken fällt auf, dass wir jedes allgemeine Dreieck durch das Einzeichnen einer Höhe in zwei rechtwinklige Dreiecke aufteilen können.
Wenn wir nun den Sinus für die beiden entstehenden rechtwinkligen Teildreiecke aufstellen, so erhalten wir:
\( \sin(α) = \frac{GK}{HY} = \frac{h_c}{b} \)
\( \sin(β) = \frac{GK}{HY} = \frac{h_c}{a} \)
Stellen wir beide Gleichungen nach hc um:
\( \sin(α) = \frac{h_c}{b} \longrightarrow h_c = b·sin(α) \)
\( \sin(β) = \frac{h_c}{a} \longrightarrow h_c = a·sin(β) \)
Als nächstes setzen wir beide Formeln für hc gleich:
hc = hc
b·sin(α) = a·sin(β)
Diese stellen wir noch wie folgt um:
\( b·\sin(α) = a·\sin(β) \quad | : \sin(α) \\ b = \frac{a·\sin(β)}{\sin(α)} \quad | : \sin(β) \\ \frac{b}{\sin(β)} = \frac{a}{\sin(α)} \)
Und das ist schon der erste Teil des Sinussatzes.
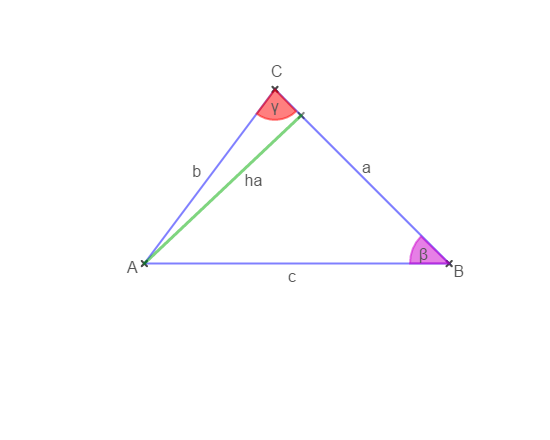
Bringen wir Seite c und sin(γ) noch in die Gleichung hinein. Wir zeichnen die Höhe ha ein und stellen danach die entsprechende Gleichung auf:
\( \sin(γ) = \frac{GK}{HY} = \frac{h_a}{b} \longrightarrow h_a = \sin(γ) · b \)
\( \sin(β) = \frac{GK}{HY} = \frac{h_a}{c} \longrightarrow h_a = \sin(β) · c \)
\( h_a = h_a \\ \sin(γ) · b = \sin(β) · c \quad | :b \text{ und } :c \\ \frac{\sin(γ)}{c} = \frac{\sin(β)}{b} \quad | \text{ Kehrwert} \\ \frac{c}{\sin(γ)} = \frac{b}{\sin(β)} \)
Und jetzt können wir in Zusammenhang bringen, wenn
\( \frac{a}{\sin(α)} = \frac{b}{\sin(β)} \quad \text{ und } \quad \frac{c}{\sin(γ)} = \frac{b}{\sin(β)}, \)
dann gilt:
$$ \frac{a}{\sin(α)} = \frac{b}{\sin(β)} = \frac{c}{\sin(γ)} $$
Dies ist der vollständige Sinussatz.