Lektion DIF02: Grafisches Ableiten / Einführung zur Ableitung
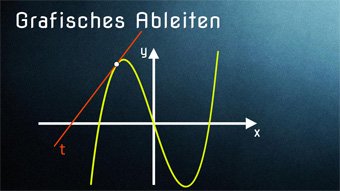
Grafisches Ableiten (Einführung zur Ableitung)
Was ist ein Ableitung und wie kann man einen Graphen grafisch ableiten. Was ist die Steigung in einem Punkt und was hat eine Tangente bzw. Steigungstangente damit zu tun. Wir erstellen grafisch die Ableitungsfunktion am Beispiel der quadratischen Funktion. Auch lernen wir Hochpunkte und Tiefpunkte kennen.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
DIF02-2 Grafisches Ableiten (Beispiele)Wie werden die Graphen von kubischen Funktionen grafisch abgeleitet. Wie werden Sinus- und Kosinusfunktion grafisch abgeleitet.
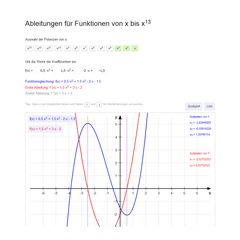
Hier findet ihr ein Programm für die Ableitung von Polynomfunktionen, einfach Funktionsgleichung eingeben und der Graph sowie der Graph der Ableitungsfunktion werden euch angezeigt: Programm zu Ableitungen für Funktionen von x bis x13
Die in den Videos eingesetzten Programme findet ihr bei:
- Graph einer quadratischen Funktion und Graph der Ableitungsfunktion
- Graph einer kubischen Funktion und Graph der Ableitungsfunktion
- Graph der Sinusfunktion und deren Ableitung
- Graph der Kosinusfunktion und deren Ableitung
Hier findest du 1 Arbeitsblatt, mit dem du dein Wissen testen kannst.
Hier findest du 1 Lerncheck, mit dem du dein Wissen testen kannst.
Artikel im Wiki:
Häufige Fragen:
Finde weitere Fragen und Antworten in der Mathelounge.