Lektion G18: Zinsrechnung
Sobald ihr euer Geld auf ein Sparkonto einzahlt oder einen Kredit bei einer Bank nehmen müsst, habt ihr es mit Zinsen zu tun. Diese Lektion bringt euch die Grundlagen der Zinsrechnung bei, damit ihr im Alltag sicher mit Geld und den dazugehörigen Begriffen und Berechnungen umgehen könnt. Beachtet, dass wir es mit einfacher Verzinsung zu tun haben (das heißt, die Berechnungen erfolgen für 1 Jahr). Zum Verständnis dieser Lektion müsst ihr das Rechnen mit Prozenten kennen.
Wer sich fragt, was passiert, wenn man ein Kapital jedes Jahr aufs Neue verzinst, der sollte sich die Lektion Zinseszins anschauen. Hier benötigt ihr jedoch das Wissen über Potenzen, die wir uns in der nächsten Lektion ansehen.
Zinsrechnung - Einführung Kapital, Zinsen, Zinssatz
Was sind Kapital, Zinsen und Zinssatz und wie rechnen wir damit. Berechnung anhand von Beispielaufgaben.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
G18-2 Zinsrechnung - Kapital ermittelnBeispielaufgabe: Kapital errechnen aus Zinsen und Zinssatz.
-
G18-3 Zinsrechnung - Zeitgenaue ZinsrechnungWie berechnet man tag- und monatsgenaue Zinsen, Zins-Formeln, Beispielaufgaben, Zeitraum der Geldanlage aus gegebenen Werten ermitteln, Zählweise für Tage.
-
 Zinsrechnung: Zinsen berechnenHier könnt ihr belieibge Zinsen berechnen. Dazu werden Kapital und Zinssatz einfach miteinander multipliziert.
Zinsrechnung: Zinsen berechnenHier könnt ihr belieibge Zinsen berechnen. Dazu werden Kapital und Zinssatz einfach miteinander multipliziert. -
 Zinsrechnung: Kapital berechnenMit diesem Programm lässt sich aus dem Verhältnis von Zinsen und Zinssatz das angelegte Kapital errechnen.
Zinsrechnung: Kapital berechnenMit diesem Programm lässt sich aus dem Verhältnis von Zinsen und Zinssatz das angelegte Kapital errechnen. -
 Zinsrechnung: Zinssatz berechnenDer Zinssatz kann über das Verhältnis von ausgezahlten Zinsen zu Kapital (also indem man beide dividert) ermittelt werden.
Zinsrechnung: Zinssatz berechnenDer Zinssatz kann über das Verhältnis von ausgezahlten Zinsen zu Kapital (also indem man beide dividert) ermittelt werden. -
 Zinsrechnung komplettDie Berechnung von Zinsen, Kapital und Zinssatz kann hier nachvollzogen werden. Werte können mit Klick auf den jeweiligen Wert frei festgelegt werden.
Zinsrechnung komplettDie Berechnung von Zinsen, Kapital und Zinssatz kann hier nachvollzogen werden. Werte können mit Klick auf den jeweiligen Wert frei festgelegt werden. -
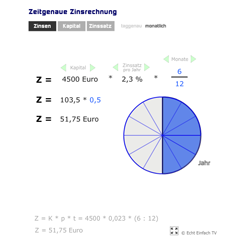 Zinsrechnung zeitgenauDie Zinsrechnung für Zinsen, Kapital und Zinssatz zeitgenau (taggenau oder monatlich). Alle Werte sind frei einstellbar.
Zinsrechnung zeitgenauDie Zinsrechnung für Zinsen, Kapital und Zinssatz zeitgenau (taggenau oder monatlich). Alle Werte sind frei einstellbar.
Hier findest du 6 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 1 Lerncheck, mit dem du dein Wissen testen kannst.
Häufige Fragen:
- Zinsaufgabe: Kapital aus gegebenen Zinsen mit Zinsformel finden?
- Berechne die Zinsen bei der Anlage eines Lottogewinns...
- Herr Meier hat 2100 und er bekommt 2142 nach 180?
- Einfache Verzinsung oder Zinsesverzinsung?
- Zinsbelastung - Monatsrate?
- Wie soll ich die Monate bei den Zinsen herausfinden?
- Welchen Betrag muss sie am Anfang des Jahres anlegen? Zinssatz 2,75 %
Finde weitere Fragen und Antworten in der Mathelounge.


