Rechner: Sinussatz
Übersicht aller RechnerDrei Werte eingeben:
Tasten ↑ und ↓ für Wertänderungen
cm cm cm Grad Grad GradDies sind die Formeln zum Berechnen von Dreiecksaufgaben mit dem Sinussatz.
Präzision mit 5 Nachkommastellen
Interaktives Dreieck
Der Sinussatz auf einen Blick
a / sin(α) = b / sin(β) = c / sin(γ)
Sinussatz-Rechner online
Herleitung vom Sinussatz
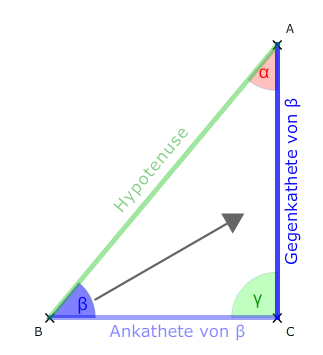
Sinus(Alpha) = Gegenkathete / Hypotenuse → kurz: sin(α) = GK/HY
Kosinus(Alpha) = Ankathete / Hypotenuse → kurz: cos(α) = AK/HY
Tangens(Alpha) = Gegenkathete / Ankathete → kurz: tan(α) = GK/AK
Stellen wir auf:
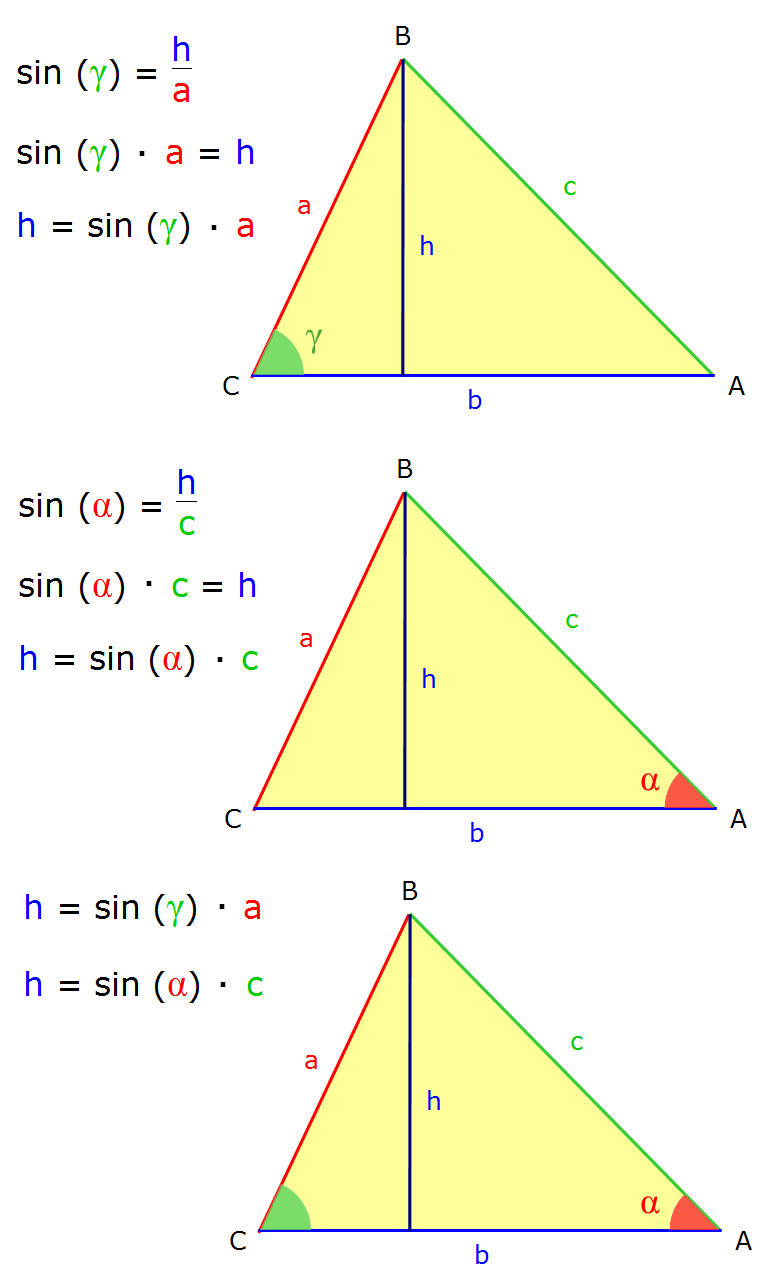
An dieser Stelle kann man gleichsetzen und erhält:
h = h
sin(γ) · a = sin(α) · c
Dann noch umstellen und wir erhalten den Sinussatz für a und c:
sin(γ) · a = sin(α) · c | :a und :c
sin(γ) : c = sin(α) : a | :a und :c
Noch als Bruch notiert:
sin(γ) / c = sin(α) / a
Entsprechend leitet man sich das Verhältnis für b und Winkel β her.
Was ist Trigonometrie?
Trigonometrie kann sinngemäß übersetzt werden als Dreiecksvermessung. Die Trigonometrie ist Teilgebiet der Geometrie und beruht auf Verhältniswerten im rechtwinkligen Dreieck. Der erste Mathematiker, der diese Verhältnisse nachweisbar dokumentiert hat, war Hipparchos (190 - 120 v.Chr.). Mehr als 600 Jahre nach ihm, hatte der Mathematiker Aryabatha (476 - 550 n.Chr.) dieses Prinzip auf rechtwinklige Dreiecke übertragen, von der unsere moderne Trigonometrie abstammt. Zur Geschichte siehe TRI01 Einführung zur Trigonometrie. Die oben im Koordinatensystem dargestellte Trigonometrie gehört zur "Ebenen Trigonometrie". Man kann die Trigonometrie aber auch auf gekrümmten Ebenen im Raum (z. B. auf einer Kugel) anwenden, dann spricht man von der "Sphärischen Trigonometrie".
Notwendiges Wissen zum Verständnis des Themas:
Beschriftungen am Dreieck: Gegenkathete, Ankathete, Hypotenuse
 als Programm aufrufen
als Programm aufrufen
Sinus-, Kosinus- und Tangenswerte sind Verhältniswerte
Unabhängig, wie ein rechtwinkliges Dreieck skaliert (also vergrößert oder verkleinert) wird, die Verhältniswerte der Seiten zueinander bleiben stets die gleichen. Auf diesem Sachverhalt beruht die Trigonometrie. Die Videos der Lektion TRI04: Sinus und Kosinus (einfach erklärt) beleuchten dies.
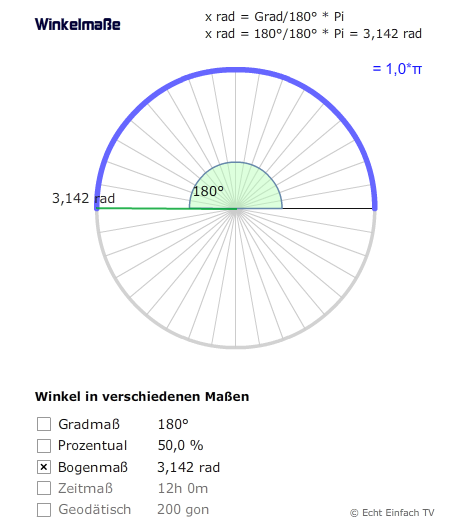
Gradmaß oder Bogenmaß
Winkel lassen sich in Grad (z. B. 180°) oder Radiant (π rad) angeben. Es gibt noch weitere Einheiten für Winkel, jedoch sind Grad und Bogenmaß die am häufigsten verwendeten.
- Sinus, Cosinus, Tangens. Kein rechter Winkel vorhanden.
- Dreiecksaufgabe mit Sinussatz lösen? Seiten a = 4 cm und b = 7,2 cm, Beta 50°
- Wann benutzt man den Sinussatz und wann den Kosinusssatz?
- Dreieck berechnen mit Sinussatz. Gegeben a=7cm c=4cm alpha=80Grad
- Dritte Seite vom allgemeinen Dreieck berechnen: a = 5 cm, b = 10 cm, Beta = 65°
- Dreieck a= 34,4m β= 38°24` ϒ= 43°48. Gesucht: 2 Seiten, 1 Winkel.
