Lektion VEK02: Vektoren bestimmen
Nachdem wir die Einführung zu den Vektoren gesehen haben und nun wissen, was ein Vektor ist, können wir mehr zum Thema kennenlernen: Wir bestimmen die Komponenten eines Vektors aus 2 Punkten. Wir lernen Verbindungs-, Orts- und Nullvektor kennen und wir betrachten uns, wie man die Vektorlänge/Vektorbetrag berechnen kann. Erfahrt alles hierzu in den Videos.
Weitere Videos für Kunden:
-
VEK02-1 Vektoren bestimmen - Verbindungsvektor, OrtsvektorWir bestimmen einen Vektor (seine Komponenten x und y) aus den Koordinaten zweier Punkte. Wir lernen die Begriffe Verbindungsvektor, Ortsvektor und Verschiebungsvektor kennen.
-
VEK02-2 Vektoren bestimmen - Vektorlänge, NullvektorDie Länge eines Vektors (auch Vektorbetrag genannt) kann mit Hilfe vom Satz des Pythagoras berechnet werden. Hierzu ziehen wir die Wurzel aus den Komponenten x² plus y². Wenn ein Vektor die Länge Null hat, sprechen wir vom Nullvektor.
Im Folgenden findet ihr die Matheprogramme aus den Videos:
-
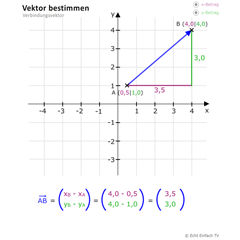 Vektor bestimmenDieses Programm berechnet die Komponenten eines Vektors aus den Koordinaten der zwei Punkte A und B. Ist der Anfangspunkt im Koordinatenursprung, so spricht man vom Ortsvektor.
Vektor bestimmenDieses Programm berechnet die Komponenten eines Vektors aus den Koordinaten der zwei Punkte A und B. Ist der Anfangspunkt im Koordinatenursprung, so spricht man vom Ortsvektor. -
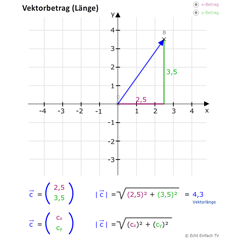 Vektorlänge (Vektorbetrag)Hier wird der Satz des Pythagoras benutzt, um die Vektorlänge zu bestimmen. Die Vektorlänge ergibt sich aus |c| = √(x²+y²).
Vektorlänge (Vektorbetrag)Hier wird der Satz des Pythagoras benutzt, um die Vektorlänge zu bestimmen. Die Vektorlänge ergibt sich aus |c| = √(x²+y²). -
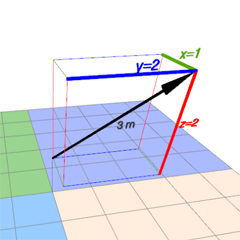 Vektoren im Raum - KomponentenMit diesem 3D-Programm kann man alle 3 Komponenten des Vektors einstellen. Zusätzlich kann die Position des Vektors verändert werden, wir sprechen dann von Orts- und Verschiebungsvektor.
Vektoren im Raum - KomponentenMit diesem 3D-Programm kann man alle 3 Komponenten des Vektors einstellen. Zusätzlich kann die Position des Vektors verändert werden, wir sprechen dann von Orts- und Verschiebungsvektor.
Hier findest du 2 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 1 Lerncheck, mit dem du dein Wissen testen kannst.
Häufige Fragen:
Finde weitere Fragen und Antworten in der Mathelounge.


