Die Höhe ist eine Strecke, die senkrecht auf eine Seite des Dreiecks gezeichnet wird und durch den darüberliegenden Punkt geht.
Zum Beispiel steht Höhe b senkrecht auf Seite b und geht durch den gegenüberliegenden Punkt B.
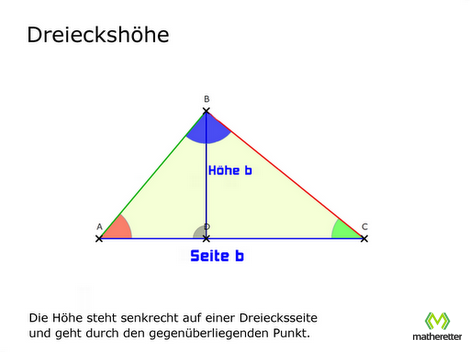
Die Höhe (sofern sie innerhalb des Dreiecks liegt) teilt jedes Dreieck in zwei rechtwinklige Dreiecke (die zueinander ähnlich sind).
Dreieckshöhen berechnen aus Seite und Winkel
Sind uns Winkel und Seite des Dreiecks gegeben, können wir diese Formeln verwenden:
ha = c · sin(β)
hb = a · sin(γ)
hc = b · sin(α)
Dreieckshöhen berechnen aus 3 Seiten
Sind uns alle drei Seiten bekannt, jedoch keine Winkel, dann können wir mit Hilfe der folgenden Formel die Strecke s berechnen und anschließend die Höhen (Herleitung erfolgt über Flächenformel):
s = 0,5 · (Seite a + Seite b + Seite c)
s = 0,5·(a+b+c)
Diese Formel verwenden wir dann wie folgt:
\( h_a = \frac{2}{a} · \sqrt{s·(s-a)·(s-b)·(s-c)} \\[10pt] h_b = \frac{2}{b} · \sqrt{s·(s-a)·(s-b)·(s-c)} \\[10pt] h_c = \frac{2}{c} · \sqrt{s·(s-a)·(s-b)·(s-c)} \)
Siehe auch Artikel Höhen im Dreieck einzeichnen.