Nachdem wir uns den Graphen in der Einführung zum Grenzwert angeschaut haben und erkannt hatten, dass sich der Grenzwert bestimmen lässt, in dem man schaut, wogegen der Graph „strebt“ (also sich annähert), wollen wir den Grenzwert nun auch rechnerisch bestimmen und mathematisch aufschreiben.
Wie erwähnt, ist die Schreibweise für den Grenzwert: lim. Als Beispiel für eine Funktion:
\( \lim \limits_{\textcolor{red}{x \to \infty}} \textcolor{blue}{\frac{x-2}{x+1}} = 1 \)
Gesprochen wird das: „Limes von f(x) für x gegen ∞ gleich 1“.
Unter dem lim stehen weitere Informationen, diese bedeuten:
- x die „Laufvariable“ - also die Variable, die wir gegen etwas streben lassen.
- → der Pfeil, der das „Streben“ ausdrückt und mit „gegen“ übersetzt wird.
- ∞ der eigentlichen Wert, gegen den wir streben: Das kann eine reelle Zahl sein oder das Unendliche.
Unendlich ∞ drückt aus, dass x gegen „sehr große Werte“ strebt.
Nach dem eigentlichen Limes lim folgt die Funktion, um die es geht.
Und nach dem Gleichheitszeichen = steht der Grenzwert.
Der Grenzwert wird allgemein so notiert: \( \lim \limits_{\textcolor{red}{x \to p}} \textcolor{blue}{f(x)} = L \)
Grenzwertregel lim 1/x = 0
Wollen wir Grenzwerte nun rechnerisch bestimmen, sollten wir uns zuvor erst klar machen, was dieses x → ∞ bedeutet.
Nehmen wir uns dazu die Funktion \(f(x) = \frac{1}{x}\) zur Hilfe. Ein Schaubild:
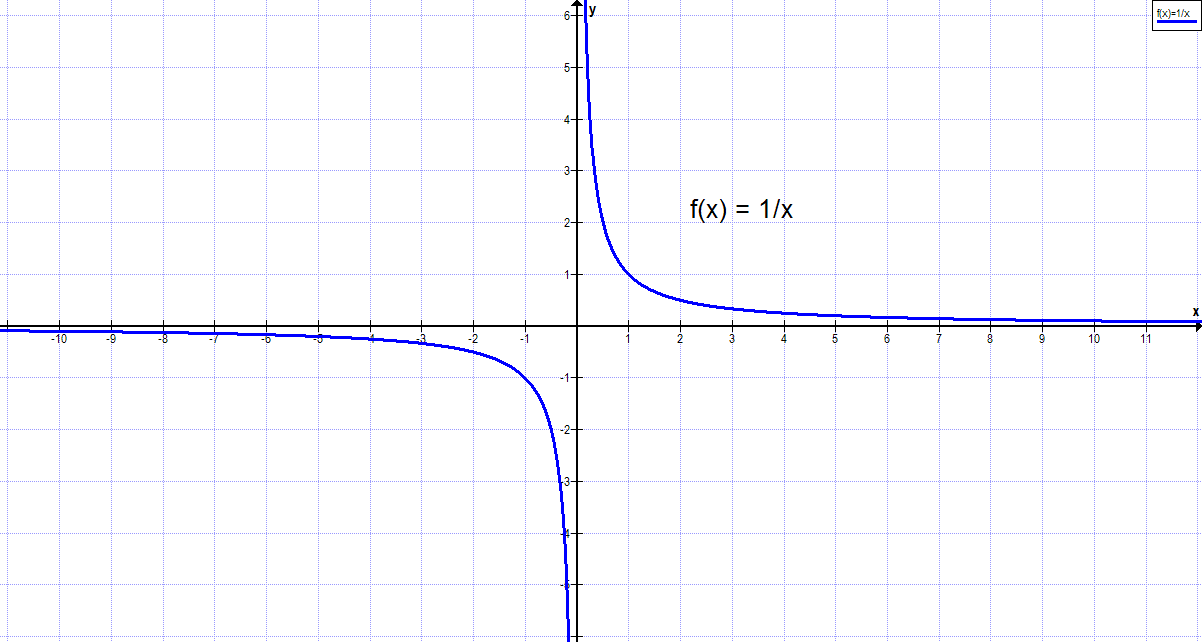
Wir sehen, dass der y-Wert für sehr große x-Werte gegen 0 geht.
Nehmen wir eine Wertetabelle zur Hilfe und setzen für x sehr große Werte ein:
| x | 1 | 100 | 10 000 | 1 000 000 | 100 000 000 |
| y | 1 | 0,01 | 0,0001 | 0,000001 | 0,00000001 |
Die Werte werden offensichtlich sehr, sehr klein. Sie streben gegen 0.
Das Verhalten von \( f(x) = \frac{1}{x} \) (gegen 0 strebend) müssen wir uns unbedingt merken, denn mit Hilfe von \( \frac{1}{x} \) lassen sich viele weitere Grenzwerte bestimmen.
Eine wichtige Grundlage für die Grenzwertberechnung ist: \( \lim \limits_{x\to \infty} \frac{1}{x} = 0 \)
Schauen wir uns einmal an, wie wir mit diesem Wissen eine Funktion rechnerisch bestimmen können:
\( \lim \limits_{x\to \infty} \frac{x-2}{x+1} = ? \)
Um hier auf den Grenzwert zu kommen, müssen wir den Bruchterm kürzen. Dabei wird vorerst je im Zähler und Nenner die höchste Potenz ausgeklammert, was hier jeweils x entspricht. Dieses x kann dann weggekürzt werden:
\( \lim \limits_{x\to \infty} \frac{x-2}{x+1} = \lim \limits_{x \to \infty} \frac{\textcolor{#00F}{x} · \left(1-\frac{2}{x}\right)}{\textcolor{#00F}{x}·\left(1+\frac{1}{x}\right)} = \lim \limits_{x \to\infty} \frac{1 -\frac{2}{x} }{1+\frac{1}{x} } \)
Nun ist es erlaubt, den Limes von Zähler und Nenner getrennt zu betrachten (wir schreiben diese Regel später nochmals separat nieder) und erkennen, dass die beiden Brüche \( \frac{2}{x} \) und \( \frac{1}{x} \) jeweils gegen 0 gehen, ganz nach unserem Musterbeispiel mit \( \frac{1}{x} \) oben. Für den Bruchterm haben wir somit:
\( \lim \limits_{x \to\infty} \frac{1 -\frac{2}{x} }{1+\frac{1}{x} } = \frac {1-0}{1+0} = \frac{1}{1} = 1 \)
\( \lim_{x\to \infty} \frac{x-2}{x+1} = 1 \)
Der Grenzwert ist mit 1 bestimmt.
Wenn wir den Graphen zeichnen, können wir dies ebenso erkennen:
~plot~ (x-2)/(x+1);1;[[-10|10|-5|5]];hide ~plot~
Hinweis: Es ist notwendig, den Limes mit lim bei den Berechnungen zu schreiben, solange er nicht angewendet ist. Das einzige Zugeständnis ist das zeitweise Weglassen des x → ∞.