Beispiel 1
Wir haben unser Eingangsbeispiel mit x gegen unendlich angeschaut. Widmen wir uns nun der Betrachtung für x gegen -unendlich. Nehmen wir dazu direkt das Eingangsbeispiel. Das Vorgehen ist dabei genau das gleiche, nur muss man das Vorzeichen berücksichtigen
\( \lim \limits_{x\to -\infty} \frac{x-2}{x+1} = \lim \limits_{x\to -\infty} \frac{x\left(1-\frac2x\right)}{x\left(1+\frac1x\right)} \)
Bei der Betrachtung der kleinen Brüche in den Klammern spielt das Vorzeichen keine Rolle. Diese Werte werden mit oder ohne Vorzeichen gegen 0 streben. Wir haben also wieder den Grenzwert 1, wie wir uns auch wieder im Graphen bestätigen lassen können.
(x+1).png)
Beispiel 2
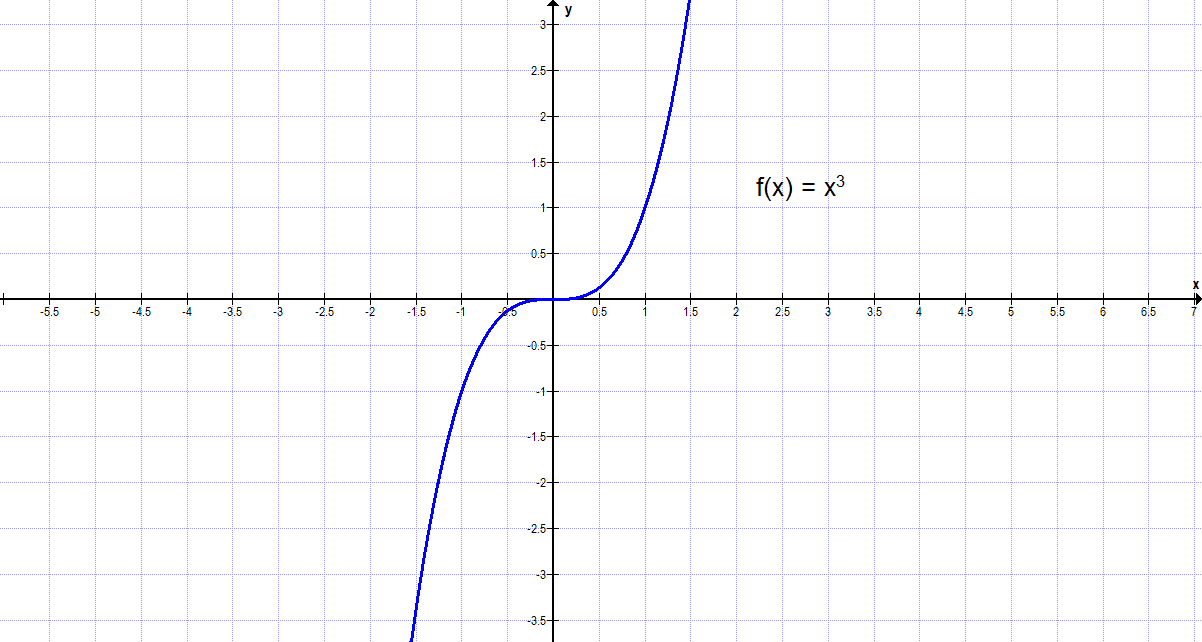
Betrachten wir noch schnell die Funktion f(x) = x³ in beide Richtungen. Wir erkennen sofort das Verhalten:
\( \lim \limits_{x \to \infty} x^3 = \infty \)
\( \lim \limits_{x \to -\infty} x^3 = \{(-\infty)^3 = -(\infty)^3\} = -\infty \)
Das in geschweiften Klammern wird so nie hingeschrieben und soll nur der Veranschaulichung dienen, dass das Vorzeichen vom Exponenten nicht ausgelöscht wird und deshalb berücksichtigt werden muss.
Hier noch der Graph: