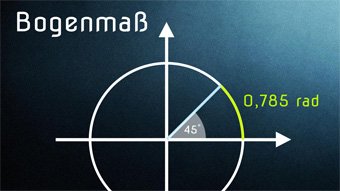
Es kann vorkommen, dass wir einen Winkel vom Gradmaß (DEG) ins Bogenmaß (RAD) umrechnen müssen.
Hierzu lässt sich eine Verhältnisgleichung aufstellen, denn es gilt:
1 Vollkreis = 360°
1 Vollkreis = 2·π ≈ 2·3,14159 ≈ 6,2832
Demnach:
360° ≙ 2·π
Beispiel: Wir wollen den Winkel 60° im Bogenmaß haben.
Nun können wir das Verhältnis wie folgt aufstellen:
\( \frac{60°}{360°} = \frac{x}{2·π} \quad |·2·π \\ 2·π·\frac{60°}{360°} = x \\ 2·π·\frac{1}{6} = x \quad | \text{Anteil ist ein Sechstel von Pi} \\ x ≈ 1,0472 \)
Wir können allgemein die Umrechnungsformel notieren:
$$ \frac{ \textcolor{blue}{\alpha} }{360°} = \frac{x}{2·π} \quad |·2·π \\ x = 2·π·\frac{\textcolor{blue}{\alpha}}{360°} $$
Jetzt müssen wir nur noch den Winkel α (Gradmaß) in die Formel einsetzen und können bequem ausrechnen.
In gleicher Weise nutzen wir die Verhältnisgleichung, wenn wir von Bogenmaß zu Gradmaß umrechnen sollen:
$$ \frac{x}{360°} = \frac{\textcolor{blue}{\alpha}}{2·π} \quad |·360° \\ x = 360°·\frac{\textcolor{blue}{\alpha}}{2·π} $$
Jetzt nur noch den Wert für Winkel α (Bogenmaß) einsetzen und den Winkel in Grad ausrechnen.