Lektion VEK05: Skalarmultiplikation
Nach der Vektoraddition und der Vektorsubtraktion folgt die Multiplikation, wir multiplizieren einen Skalar (eine Zahl) mit einem Vektor und nennen das ganze „Skalarmultiplikation“.
Warum wir die Zahl "Skalar" nennen, erfahrt ihr im Einführungsvideo.
Skalarmultiplikation - Einführung Skalar mal Vektor
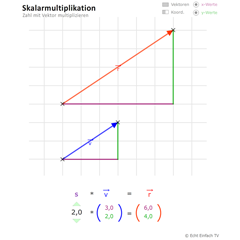
Was ist ein Skalar (Zahl), wie multiplizieren wir einen Skalar mit einem Vektor s·v=r, was bedeutet das geometrisch. Vektorlängen entsprechend des Skalars (Vektorstreckung, Vektorstauchung). Gegenvektor mit (-1)·v.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
VEK05-2 Skalarmultiplikation - RechengesetzeKommutativgesetz, Assoziativgesetz und Distributivgesetz für die Skalarmultiplikation. Geometrische Darstellung des Distributivgesetzes s·(a+b) = s·a + s·b für die Skalarmultiplikation.
Nachstehend das Programm zur Skalarmultiplikation aus den Videos:
Hier findest du 1 Arbeitsblatt, mit dem du dein Wissen testen kannst.
Hier findest du 1 Lerncheck, mit dem du dein Wissen testen kannst.