Zunächst wird die Aufgabe so modifiziert, wenn sie nicht schon als homogene Aufgabe vorliegt, dass durch Setzen von \(g(t) = 0\) die DGL homogenisiert wird.
\( \dot y\left( t \right) + a \cdot y\left( t \right) = 0 \) Gl. 236
In dieser Form kann jetzt eine Trennung der Variablen durchgeführt werden, indem das Differenzial \(\dot y\left( t \right) = \frac{ {dy} }{ {dt} }\) formal wie ein Quotient betrachtet wird:
\( \frac{ {dy} }{ {dt} } + a \cdot y = 0 \) Gl. 237
Trennung der Variablen
\( \frac{ {dy} }{y} = - a \cdot dt \) Gl. 238
Nunmehr kann auf beiden Seiten eine unbestimmte Integration angewendet werden
\( \int {\frac{ {dy} }{y} } = - a \cdot \int {dt} \) Gl. 239
also \(\ln \left( y \right) + C = - at\) und schließlich
\( y = K \cdot {e^{ - at} } \) Gl. 240
Wie bei jeder Integration, darf auch hier nicht das Hinzufügen einer unbestimmten Konstante vergessen werden, da diese ja bei der Differenziation verschwindet. Diese Konstante wird dazu benutzt, gewisse Randbedingungen in die Lösung einzuarbeiten.
Weil die Lösung der Differenzialgleichung durch Integration erfolgt, werden die Lösungen von Differenzialgleichungen auch Integrale der DGL genannt.
Beispiel:
Die Bestimmung der Flughöhe von Flugzeugen kann durch Messung des Luftdruckes nach der barometrischen Höhenformel erfolgen.
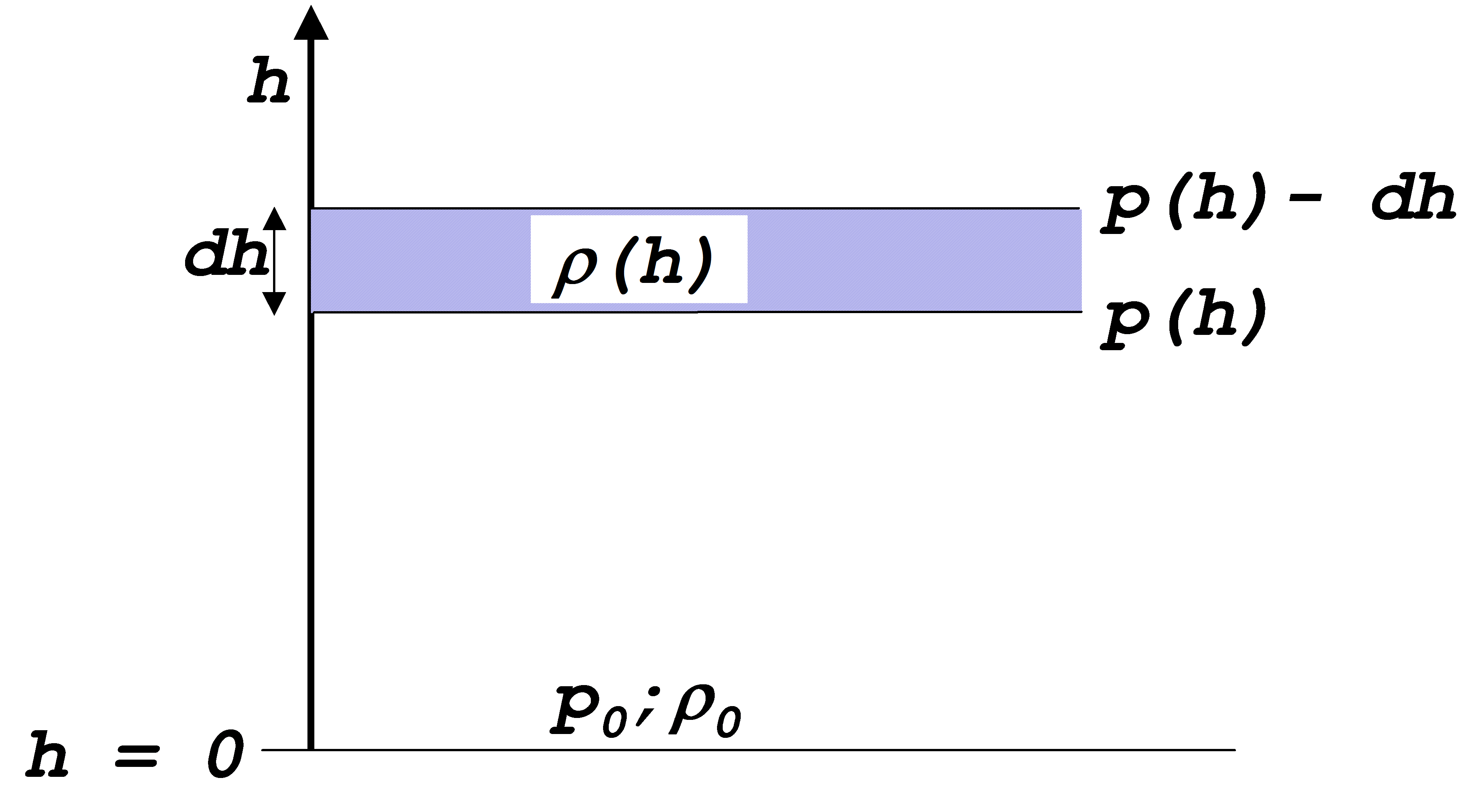
Zur Bestimmung der Abhängigkeit des Luftdruckes von der Höhe wird eine dünne Schicht der Atmosphäre betrachtet. In der Höhe h wirke der Luftdruck p(h). Mit steigender Höhe verringert sich der Luftdruck, so dass die Änderung des Luftdruckes sich gegensinnig zur Höhe verändert. Es gilt also
\(dp = - \rho \left( h \right) \cdot g \cdot dh\)
wenn r die Dichte der Luft in der Höhe h und g die Erdbeschleunigung ist.
Da die Dichte aber nicht bekannt ist, muss ein physikalischer Zusammenhang zwischen Druck und Dichte gefunden werden, dieser ist durch das Boyle-Marriotesche Gesetz gegeben
\(\frac{p}{ { {p_0} } } = \frac{\rho }{ { {\rho _0} } }\) \({p_0}\) und \({\rho _0}\) werden geeigneter Weise als Druck und Dichte in Höhe des Erdbodens (h=0) gewählt.
Jetzt kann die Differenzialgleichung aufgestellt und gelöst werden
\(dp = - p\frac{ { {\rho _0} } }{ { {p_0} } } \cdot g \cdot dh\)
\(\frac{ {dp} }{p} = - \frac{ { {\rho _0} } }{ { {p_0} } } \cdot g \cdot dh\)
\(p = K \cdot {e^{ - \frac{ { {\rho _0} } }{ { {p_0} } } \cdot gh} }\)
Bis auf die Konstante K ist der funktionelle Zusammenhang zwischen Druck und Höhe gegeben. Zur Bestimmung der Konstanten wird jetzt eine Randbedingung eingeführt, nämlich, dass der Luftdruck in der Höhe h=0 p0 betragen soll:
\({p_0} = K \cdot {e^0} = K\) damit folgt die vollständige barometrische Formel
\(p = {p_0} \cdot {e^{ - \frac{ { {\rho _0} } }{ { {p_0} } } \cdot gh} }\)
