Eine inhomogene DGL wird mit Hilfe eines Ansatzes gelöst. Dabei wird die Lösung der homogenen DGL mit einer partikulären Lösung, die die inhomogene DGL erfüllt, überlagert.
\(y\left( t \right) = {y_h}\left( t \right) + {y_p}\left( t \right)\) Gl. 241
Die partikuläre Lösung wird durch Variation der Konstanten nach LAGRANGE (Joseph-Louis, 1736-1813) erhalten.
Wenn \({y_h}\left( t \right) = K \cdot {e^{ - at} }\) die Lösung der homogenen Aufgabe ist, wird jetzt die Konstante K ebenfalls als Variable betrachtet:
\( {y_h}\left( t \right) = K\left( t \right) \cdot {e^{ - at} } \) Gl. 242
Dieser Term wird nun die inhomogene Aufgabe eingesetzt. Dabei ist zu beachten, dass beide Faktoren nach der Produktregel zu differenzieren sind:
\( {\dot y_h}\left( t \right) = \dot K\left( t \right) \cdot {e^{ - at} } - a \cdot K\left( t \right) \cdot {e^{ - at} } \) Gl. 243
\(\begin{array}{l}\dot y\left( t \right) \qquad + a \cdot y\left( t \right)\,\,\,\,\,\,\,\,\,\,\,\,\, = g(t) \\ \dot K\left( t \right) \cdot {e^{ - at} } - a \cdot K\left( t \right) \cdot {e^{- at} } + a \cdot K\left( t \right) \cdot {e^{ - at} } = g(t)\end{array} \) Gl. 244
Vorteilhafter Weise verschwinden die Beiträge der homogenen Lösung, da die homogene Lösung ja die Lösung einer DGL ist, deren Störung zu Null gesetzt wurde.
\( \dot K\left( t \right) \cdot {e^{ - at} } = g(t) \) Gl. 245
umstellen
\( \dot K\left( t \right) = g(t) \cdot {e^{at} } \) Gl. 246
und Lösen durch Integration nach Trennung der Variablen
\( dK = \left( {g(t) \cdot {e^{at} } } \right)dt \) Gl. 247
\( K = \int {\left( {g(t) \cdot {e^{at} } } \right)dt + C} \) Gl. 248
Auch diese Integration liefert wieder eine Konstante, die ebenfalls durch Einarbeitung einer Randbedingung bestimmt werden kann.
Wird jetzt diese „Konstante“ in die ursprüngliche Lösung der homogenen Aufgabe eingesetzt, zeigt sich, dass die Lösung der inhomogenen Aufgabe tatsächlich als Superposition beider Aufgaben, der homogenen und der inhomogenen, darstellt:
\( y\left( t \right) = \left[ {\int {\left( {g(t) \cdot {e^{at} } } \right)dt + C} } \right] \cdot {e^{ - at} } = {e^{ - at} }\int {\left( {g(t) \cdot {e^{at} } } \right)dt + C \cdot {e^{ - at} } } \) Gl. 249
Beispiel:
Das im Beispiel gezeigte massefreie, frei bewegliche Federsystem (z.B. PKW-Stoßdämpfer im nichteingebauten Zustand) wird durch eine Reibung gedämpft. Die Kräftebilanz lautet

\({F_a}\left( t \right) = r \cdot \dot x + n \cdot x\)
Normieren auf die Reibungskonstante r ergibt die inhomogene DGL, deren Lösung für eine bestimmte äußere Kraft gesucht ist.
\(\frac{ { {F_a}\left( t \right)} }{r} = \dot x + \frac{1}{\tau } \cdot x\)
Worin \(\tau = \frac{r}{n}\) die Zeitkonstante des Systems darstellt.
1. Bestimmung der homogenen Aufgabe
\(\dot x + \frac{1}{\tau } \cdot x = 0\)
Nach Gl. 240 lautet die homogene Lösung
\(x\left( t \right) = K \cdot {e^{ - \frac{t}{\tau } } }\)
2. Lösung der inhomogenen Aufgabe
Gegeben sei:
\({F_a}\left( t \right) = \hat F \cdot \sin \left( {\omega \cdot t} \right)\)
worin \(\omega = 2\pi \cdot f\) die Anregungsfrequenz der äußeren Kraft bedeutet.
Die LAGRANGE’sche Variation der Konstanten ergibt
\(\frac{ {\hat F \cdot \sin \left( {\omega \cdot t} \right)} }{r} = \dot K\left( t \right) \cdot {e^{ - \frac{t}{\tau } } } - \frac{1}{\tau } \cdot K\left( t \right) \cdot {e^{ - \frac{t}{\tau } } } + \frac{1}{\tau } \cdot K\left( t \right) \cdot {e^{ - \frac{t}{\tau } } } = \dot K\left( t \right) \cdot {e^{ - \frac{t}{\tau } } }\)
Trennung der Variablen
\( \frac{ {\hat F \cdot \sin \left( {\omega \cdot t} \right)} }{r} = \frac{ {dK} }{ {dt} } \cdot {e^{ - \frac{t}{\tau} } } \quad \Rightarrow \quad dK = \frac{ {\hat F \cdot \sin \left( {\omega \cdot t} \right)} }{r} \cdot {e^{\frac{t}{\tau } } } \cdot dt \) oder
\( K\left( t \right) = \frac{ {\hat F} }{r} \cdot \int {\sin \left( {\omega \cdot t} \right) \cdot {e^{\frac{t}{\tau } } } \cdot dt} + C = \frac{ {\hat F} }{r} \cdot \frac{ { {\tau^2} } }{ {1 + { {\left( {\tau \cdot \omega } \right)}^2} } } \cdot \left( {\frac{1}{\tau }\sin \left( {\omega \cdot t} \right) - \omega \cdot \cos \left( {\omega \cdot t} \right)} \right) \cdot {e^{\frac{t}{\tau } } } + C \)
Einsetzen in die homogene Lösung
\( x\left( t \right) = \left[ {\frac{ {\hat F} }{r} \cdot \frac{ { {\tau ^2} } }{ {1 + { {\left( {\tau \cdot \omega } \right)}^2} } } \cdot \left( {\frac{1}{\tau }\sin \left( {\omega \cdot t} \right) - \omega \cdot \cos \left( {\omega \cdot t} \right)} \right) \cdot {e^{\frac{t}{\tau } } } + C} \right] \cdot {e^{ - \frac{t}{\tau } } } \)
\( x\left( t \right) = \frac{ {\hat F} }{r} \cdot \frac{ { {\tau^2} } }{ {1 + { {\left( {\tau \cdot \omega } \right)}^2} } } \cdot \left( {\frac{1}{\tau }\sin \left( {\omega \cdot t} \right) - \omega \cdot \cos \left( {\omega \cdot t} \right)} \right) + C \cdot {e^{ - \frac{t}{\tau } } } \)
Zur Bestimmung der Konstanten C wird angenommen, dass x(0)=0 ist
\( 0 = \frac{ {\hat F} }{r} \cdot \frac{ { - \omega \cdot {\tau^2} } }{ {1 + { {\left( {\tau \cdot \omega } \right)}^2} } } + C \quad \Rightarrow \quad C = \frac{ {\hat F} }{ {\omega \cdot r} } \cdot \frac{ { { {\left( {\omega \cdot \tau } \right)}^2} } }{ {1 + { {\left( {\tau \cdot \omega } \right)}^2} } } \)
Damit lautet die vollständige Lösung
\(x\left( t \right) = \frac{ {\hat F} }{ {\omega \cdot r} } \cdot \frac{ { { {\left( {\omega \cdot \tau } \right)}^2} } }{ {1 + { {\left( {\tau \cdot \omega } \right)}^2} } } \cdot \left( {\frac{1}{ {\omega \cdot \tau } }\sin \left( {\omega \cdot t} \right) - \cos \left( {\omega \cdot t} \right) + {e^{ -\frac{t}{\tau } } } } \right)\)
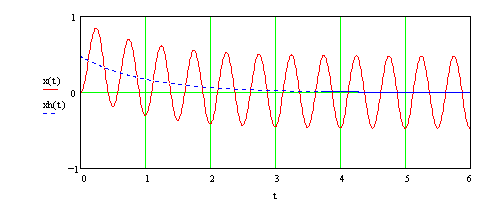
Der Ausdruck \(\frac{ {\hat F} }{ {\omega \cdot r} } \cdot \frac{ { { {\left( {\omega \cdot \tau } \right)}^2} } }{ {1 + { {\left( {\tau \cdot \omega } \right)}^2} } } \cdot {e^{ -\frac{t}{\tau } } }\) stellt die homogene Lösung dar, die, weil ihr Einfluss mit größer werdendem t abnimmt, auch flüchtiger Zustand genannt wird.
Der Beitrag der inhomogenen Lösung ist dem der homogenen additiv überlagert, er bleibt über alle Zeit erhalten und wird deshalb eingeschwungener Zustand genannt.
Bei sinusförmiger Erregung (Störung) des Feder-Reibungs-Systems kann die Superposition von homogener Lösung (gestrichelt) und inhomogener Lösung (rote Linie) gut verfolgt werden. Während die homogene Lösung flüchtig ist, bleibt die inhomogene Lösung als eingeschwungener Zustand erhalten.