Bekanntlich hat nach Aussage des Fundamentalsatzes der Algebra jedes Polynom n. Grades auch n Nullstellen. Dabei können die Nullstellen reell, komplex (wie im vorangegangenen Beispiel) oder mehrfach sein. Reelle oder komplexe Nullstellen führen stets auf die erforderliche Anzahl von partikulären Lösungen zur Bestimmung der allgemeinen Lösung der DGL.
Anders bei den mehrfachen Nullstellen. Diese hätten mehrfach den gleichen Wert, würden somit keine unabhängigen Lösungen liefern.
Es kann nachgewiesen werden, dass in diesen Fällen auch Produkte der mehrfachen Lösung mit der unabhängigen Variablen zu unabhängigen partikulären Lösungen führen.
Es sei lm eine m-fache Nullstelle eines charakteristischen Polynoms n. Ordnung (m ≤ n), dann sind
\( {y_1}\left( t \right) = {e^{ {\lambda _n}t} },\,\,{y_2}\left( t \right) = t \cdot {e^{ {\lambda _n}t} },\,\,{y_3}\left( t \right) = {t^2} \cdot {e^{ {\lambda _n}t} },\,\,{y_m}\left( t \right) = {t^{\left( {m - 1} \right)} } \cdot {e^{ {\lambda _n}t} } \) Gl. 259
ebenfalls partikuläre Lösungen der DGL.
Beispiel:
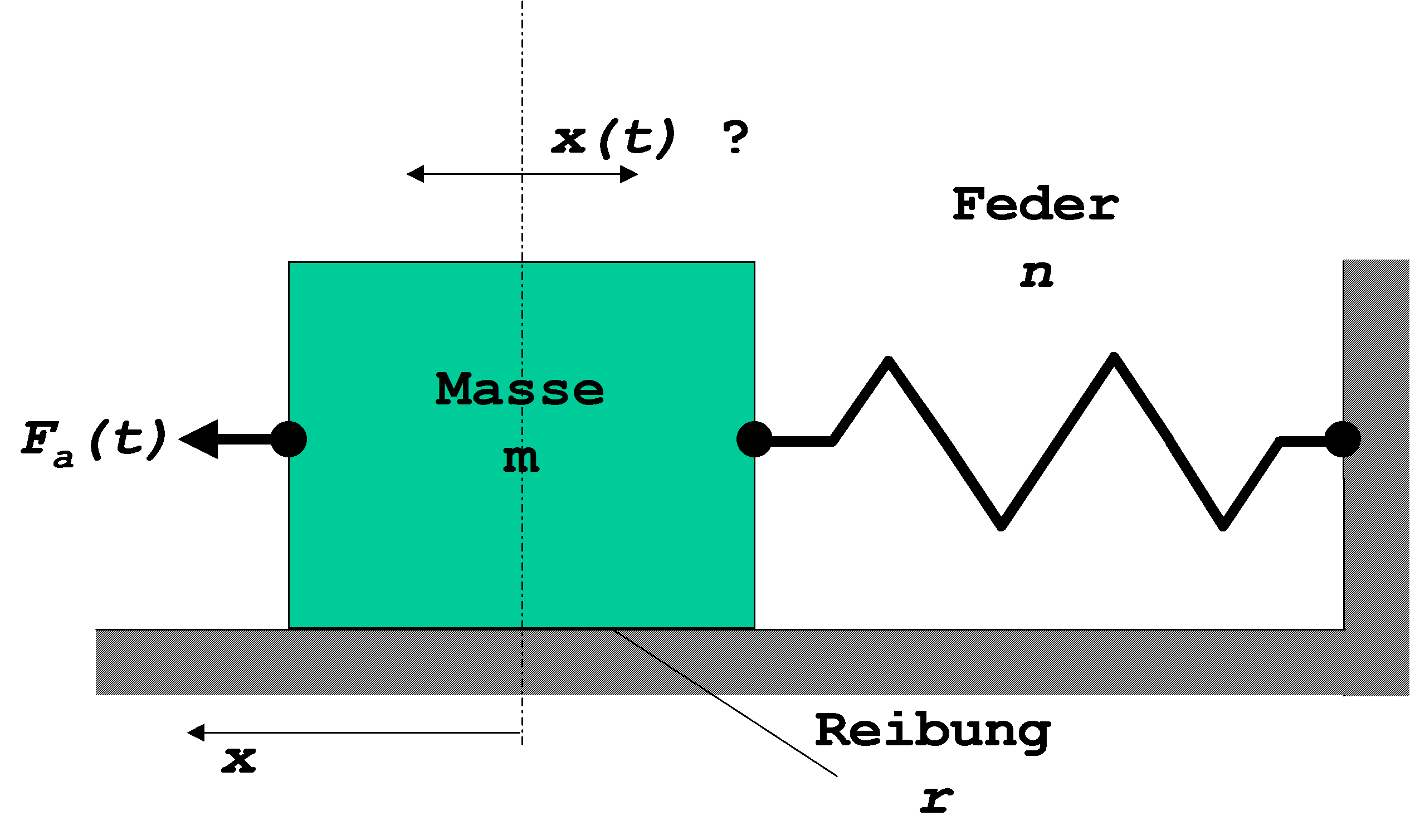
Die Differenzialgleichung zu der Grafik lautet:
\({F_a}\left( t \right) = m \cdot \ddot x + r \cdot \dot x + n \cdot x\)
Der Einfachheit halber soll angenommen werden, dass auf die Masse m keine äußere Kraft einwirkt, mit Ausnahme einer Anfangsauslenkung x0. Zusätzlich befinde sich das System zu diesem Zeitpunkt in Ruhe, d.h. \(\dot x = 0\). Ab dem Zeitpunkt t = 0 wird das System sich selbst überlassen. Mit dieser Einschränkung liegt eine homogene DGL vor, die durch Anfangsbedingungen an die gegebenen Bedingungen angepasst wird. Es ist also die DGL
\(m \cdot \ddot x + r \cdot \dot x + n \cdot x = 0\)
zu lösen.
Mit dem Ansatz nach Gl. 254 \(x\left( t \right) = {e^{\lambda t} }\) lautet das charakteristische Polynom
\(m \cdot {\lambda ^2} + r \cdot \lambda + n = 0\)
Division durch m und Substitution von
\(\frac{r}{m} = 2\delta \) (d: Dämpfung) und \(\frac{n}{m} = \omega _0^2\) (w0: Resonanzfrequenz des Systems)
ergibt:
\({\lambda ^2} + 2\delta \cdot \lambda + \omega _0^2 = 0\)
Die Nullstellen dieser quadratischen Gleichung nach dem Wurzelsatz von Vieta lauten:
\( {\lambda _{1,2} } = - \delta \pm \sqrt { {\delta ^2} - \omega _0^2} \)
Mit diesen Werten können jetzt die partikulären Lösungen der homogenen DGL berechnet und zur allgemeinen Lösung summiert werden.
\( x\left( t \right) = {c_1} \cdot {e^{ {\lambda _1}t} } + {c_2} \cdot {e^{ {\lambda _2}t} } \)
Mit der Anfangsbedingung \(x\left( 0 \right) = {x_0}\) und \(\dot x\left( 0 \right) = 0\) werden die Konstanten bestimmt:
a) \(x\left( 0 \right) = {c_1} + {c_2} = {x_0}\)
b) \(\dot x\left( 0 \right) = {c_1} \cdot {\lambda _1} + {c_2} \cdot {\lambda _2} = 0\)
also
\({c_1} = - {x_0}\frac{ { {\lambda _2} } }{ { {\lambda _1} - {\lambda _2} } } = {x_0}\frac{ {\delta + \sqrt { {\delta ^2} - \omega _0^2} } }{ {2 \cdot \sqrt { {\delta ^2} - \omega _0^2} } }\) und
\({c_2} = {x_0}\frac{ { {\lambda _1} } }{ { {\lambda _1} - {\lambda _2} } } = {x_0}\frac{ { - \delta + \sqrt { {\delta ^2} - \omega _0^2} } }{ {2 \cdot \sqrt { {\delta ^2} - \omega _0^2} } }\) ⇒
\(x\left( t \right) = \frac{ { {x_0} \cdot {e^{ - \delta t} } } }{ {2 \cdot \sqrt { {\delta ^2} - \omega _0^2} } }\left( {\left( {\delta + \sqrt { {\delta ^2} - \omega _0^2} } \right) \cdot {e^{\sqrt { {\delta ^2} - \omega _0^2} \cdot t} } + \left( { - \delta + \sqrt { {\delta ^2} - \omega _0^2} } \right) \cdot {e^{ - \sqrt { {\delta ^2} - \omega _0^2} \cdot t} } } \right)\)
Nun sind drei Fälle der Lösung zu unterscheiden:
1. \( \delta > {\omega _0}\), die Wurzel ist reell und die Lösung lautet
\( x\left( t \right) = \frac{ { {x_0}{e^{ -\delta t} } } }{ {2\Delta } }\left( {\left( {\delta + \Delta } \right) \cdot {e^{\Delta t} } + \left( { - \delta + \Delta } \right) \cdot {e^{ - \Delta t} } } \right); \quad \Delta = \sqrt { {\delta ^2} - \omega _0^2} \)
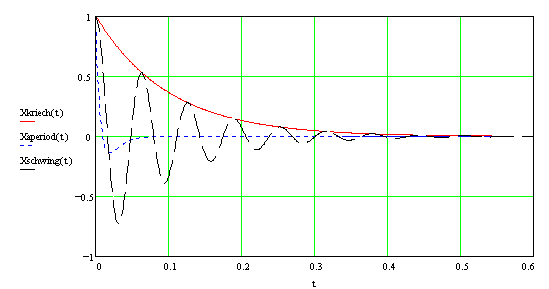
Dieser Fall wird Kriechfall genannt (siehe Abbildung 30).
2. \(\delta < {\omega _0}\), die Wurzel wird imaginär und führt zu folgender Lösung
\( x\left( t \right) = \frac{ { {x_0}{e^{ - \delta t} } } }{ {2i \cdot \Delta } }\left( {\left( {\delta + i \cdot \Delta } \right) \cdot {e^{i\Delta t} } + \left( { - \delta + i \cdot \Delta } \right) \cdot {e^{ - i\Delta t} } } \right); \quad \Delta = \sqrt {\omega _0^2 - {\delta ^2} } \)
\( x\left( t \right) = {x_0}{e^{ - \delta t} }\left( {\cos \left( {\Delta t} \right) + \frac{\delta }{\Delta }\sin \left( {\Delta t} \right)} \right) \)
Dieser Fall wird Schwingfall genannt.
3. \(\delta = {\omega _0}\) es liegt eine zweifache Wurzel vor \(\left( {\Delta = 0!} \right)\) und die Lösung lautet
\( x\left( t \right) = {c_1} \cdot {e^{\delta t} } + {c_2} \cdot t \cdot {e^{\delta t} } \)
Die Bestimmung der Konstanten erfolgt wieder anhand der gegebenen Anfangsbedingungen. Aus \(x\left( 0 \right) = {x_0}\) und \(\dot x\left( 0 \right) = 0\) folgt:
a) \(x\left( 0 \right) = {c_1} = {x_0}\)
b) \(\dot x\left( 0 \right) = {c_1} \cdot \delta + {c_2} = 0\) also
\( {c_1} = {x_0}\) und \({c_2} = - \delta {x_0} \) ⇒
\( x\left( t \right) = {x_0} \cdot {e^{ - \delta t} }\left( {1 - \delta \cdot t} \right) \)
Dieser Fall wird aperiodischer Grenzfall genannt.