Audio-Fingerabdrücke unterscheiden sich von standardmäßigen Computer-Fingerabdrücken wie SSHA oder MD5, da zwei verschiedene Dateien (in Bezug auf Bits), die die gleiche Musik enthalten, den gleichen Audio-Fingerabdruck haben müssen. Zum Beispiel muss ein Song in einem 256 kbit ACC-Format (iTunes) den gleichen Fingerabdruck ergeben wie in einem 256 kbit MP3 Format (Amazon) oder in einem 128 kbit WMA Format (Microsoft). Um dieses Problem zu lösen, verwenden Audio-Fingerabdruck-Algorithmen das Spektrogramm von Audiosignalen, um Fingerabdrücke zu extrahieren.
Spektrogramm erzeugen
Wir hatten bereits gesagt, dass eine FFT angewendet werden muss, um ein Spektrogramm von einem digitalen Sound zu erzeugen. Für einen Fingerabdruck-Algorithmus benötigen wir eine gute Frequenzauflösung (z. B. 10,7 Hz), um 1. Spektrumlecks* zu reduzieren und 2. die wichtigsten Noten innerhalb des Songs herauszufiltern. Gleichzeitig müssen wir die Rechenzeit so weit wie möglich reduzieren und daher die kleinstmögliche Fenstergröße verwenden.
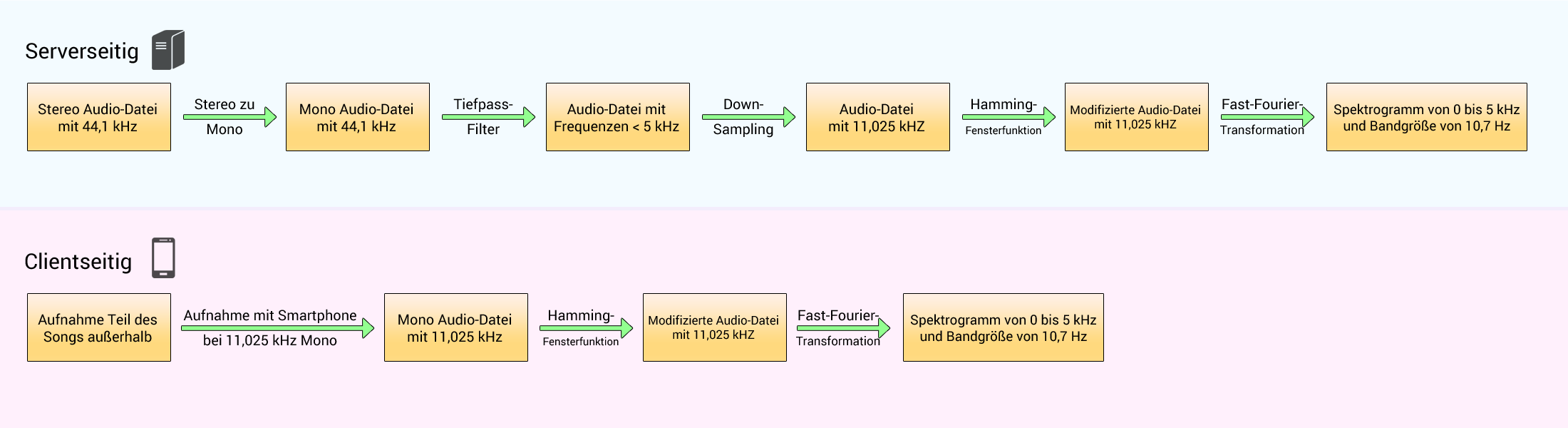
Im Paper von Shazam wird nicht erklärt, auf welche Weise man das Spektrogramm erhält, aber hier sei eine Möglichkeit gezeigt:
Auf der Serverseite (Shazam) muss der 44,1 kHz-gesampelte Sound (von CD, MP3 oder einem anderen Soundformat) von Stereo zu Mono übergehen. Wir können das tun, indem wir den Durchschnitt des linken und des rechten Lautsprechers nehmen. Vor dem Downsampling müssen wir die Frequenzen oberhalb von 5 kHz herausfiltern, um Aliasing zu vermeiden. Dann kann der Ton bei 11,025 kHz heruntergemischt (Downsampling) werden.
Auf der Clientseite (Smartphone) muss die Abtastrate des Mikrofons (Sampling rate), das den Ton aufzeichnet, bei 11,025 kHz liegen.
Dann müssen wir in beiden Fällen eine Fensterfunktion auf das Signal anwenden (wie ein Hamming 1024-Sample-Fenster, Grund hierfür siehe Kapitel Fensterfunktion) sowie die FFT für jede 1024 Samples. Auf diese Weise analysiert jede FFT 0,1 Sekunden Musik. Dies gibt uns ein Spektrogramm mit folgenden Eigenschaften:
- von 0 Hz zu 5000 Hz,
- mit einer Bandgröße von 10,7 Hz,
- 512 möglichen Frequenzen,
- einer Zeiteinheit von 0,1 Sekunden.
Filtern
An dieser Stelle haben wir das Spektrogramm des Songs. Da Shazam geräuschtolerant sein muss, werden nur die lautesten Töne beibehalten. Doch es ist noch nicht genug, nur die X stärksten Frequenzen alle 0,1 Sekunden beizubehalten. Hier sind einige Gründe:
- Zu Beginn des Artikels hatten wir über psychoakustische Modelle gesprochen. Menschliche Ohren hören einen tiefen Ton (< 500 Hz) schlechter als einen mittleren Ton (500 Hz - 2000 Hz) oder einen hohen Ton (> 2000 Hz). Als Folge dessen werden tiefe Klänge vieler „roher“ Songs künstlich erhöht, bevor sie veröffentlicht werden. Wenn man nur die stärksten Frequenzen verwenden würde, so würde man nur die tiefen Frequenzen erhalten, und wenn 2 Songs die gleiche Drum-Partition haben, kann es passieren, dass beide nach der Filterung ein sehr ähnliches Spektrogramm aufweisen, obwohl Flöten im ersten Song und Gitarren im zweiten Song spielen.
- Wir hatten bei den Fensterfunktionen gesehen, dass, wenn man eine sehr starke Frequenz hat, andere starke Frequenzen in der Nähe des Spektrums auftreten können, obwohl sie gar nicht existieren (Spektrumleck). Man muss also einen Weg finden, nur die echten Frequenzen beizubehalten.
Hier ist eine einfache Möglichkeit, nur starke Frequenzen beizubehalten und gleichzeitig die vorgenannten Probleme zu verringern:
Schritt 1 – Für jedes FFT-Ergebnis setzt man die 512 Bänder in 6 logarithmische Bänder:
- der sehr tiefe Klangbereich (von Band 0 bis 10)
- der tiefe Klangbereich (von Band 10 bis 20)
- der tiefe-mittlere Klangbereich (von Band 20 bis 40)
- der mittlere Klangbereich (von Band 40 bis 80)
- der mittlere-hohe Klangbereich (von Band 80 bis 160)
- der hohe Klangbereich (von Band 160 bis 511)
Schritt 2 – Für jedes Band behält man nur das stärkste Band der Frequenzen.
Schritt 3 – Dann berechnet man den Durchschnittswert dieser 6 stärksten Bänder.
Schritt 4 – Man behält die Bänder (von den 6 Bändern), die sich über diesem Durchschnitt befinden (multipliziert mit einem Koeffizienten).
Der letzte Schritt ist äußerst wichtig, da folgende Fälle auftreten können:
- Acapella-Musik mit Sopransängern, die nur mittlere und mittlere-hohe Frequenzen enthält.
- Jazz-/Rap-Musik mit nur tiefen und tiefen-mittleren Frequenzen.
- ...
Außerdem wollen wir keine schwache Frequenz in einem Band behalten, nur weil sie die stärkste innerhalb ihres Bandes ist.
Dieser Algorithmus hat jedoch eine Einschränkung. In den meisten Songs sind einige Teile sehr schwach, so zum Beispiel der Anfang oder das Ende eines Songs. Wenn man diese Teile analysiert, erhält man falsche starke Frequenzen, weil der Mittelwert (berechnet in Schritt 3) dieser Teile sehr niedrig ist. Um das zu vermeiden, kann man, anstatt den Mittelwert der 6 stärksten Bänder der aktuellen FFT zu nehmen (das entspricht nur 0,1 Sekunden des Songs), den Mittelwert der stärksten Bänder des gesamten Songs nehmen.
Fazit: Indem wir diesen Algorithmus benutzen, filtern wir das Spektrogramm des Songs und behalten die Frequenzspitzen (Peaks) im Spektrum bei, die die lautesten Noten repräsentieren. Um eine Vorstellung davon zu haben, was diese Filterung macht, sei nachstehend ein echtes Spektrogramm eines 14-Sekunden-Songs gezeigt.
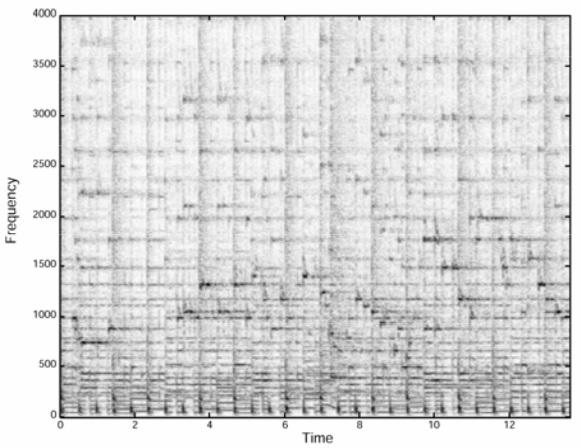
Diese Abbildung stammt aus dem Shazam-Paper. In diesem Spektrogramm kann man sehen, dass einige Frequenzen stärker sind als andere. Wenn man den vorgenannten Algorithmus auf das Spektrogramm anwendet, erhält man Folgendes:
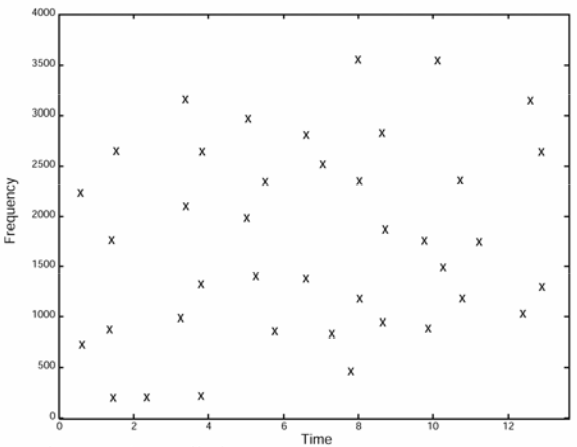
Diese Abbildung (siehe auch Shazam-Paper) zeigt ein gefiltertes Spektrogramm. Nur die stärksten Frequenzen aus der vorherigen Abbildung werden beibehalten. Einige Teile des Songs haben nach der Filterung keine Frequenz mehr (zum Beispiel zwischen 4 und 4,5 Sekunden).
Die Anzahl der Frequenzen im gefilterten Spektrogramm hängt von dem Koeffizienten ab, der bei Schritt 4 mit dem Mittelwert verwendet wurde. Sie hängen auch von der Anzahl der Bänder ab, die man verwendet (wir haben 6 Bänder verwendet, aber wir hätten auch eine andere Zahl wählen können).
An dieser Stelle ist die Intensität der Frequenzen nutzlos. Daher kann dieses Spektrogramm als zweispaltige Tabelle modelliert werden, bei der:
- die erste Spalte die Frequenz in dem Spektrogramm darstellt (y-Achse)
- die zweite Spalte die Zeit darstellt, zu der die Frequenz während des Songs auftritt (x-Achse)
Dieses gefilterte Spektrogramm ist nicht der endgültige Audio-Fingerabdruck, aber es ist bereits ein großer Teil davon. Im nächsten Kapitel erfahren wir mehr darüber.
Hinweis: Wir haben gerade einen einfachen Algorithmus kennengelernt, um das Spektrogramm zu filtern. Ein besserer Ansatz könnte darin bestehen, ein logarithmisches Gleitfenster zu verwenden und nur die stärksten Frequenzen über dem Mittelwert + der Standardabweichung (multipliziert mit einem Koeffizienten) eines sich bewegenden Teils des Songs zu behalten. Dieser Ansatz ist jedoch schwieriger zu erklären.