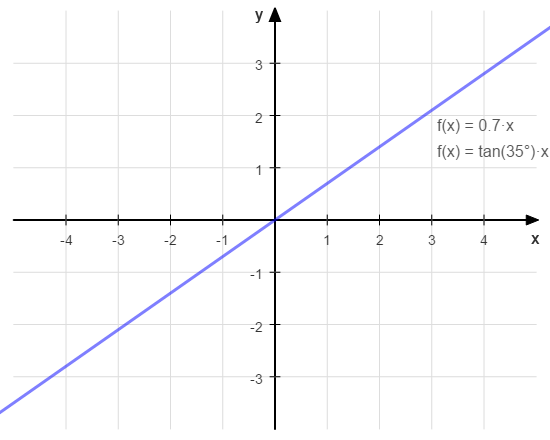
Der Tangenswert entspricht der Steigung. Beispiel: tan(35°) = 0,7.
Das heißt, wenn die Hypotenuse ein linearer Funktionsgraph wäre, dann würde dieser mit 0,7 steigen.
Die Funktionsgleichung würde lauten: f(x) = 0,7·x
Statt wie bei den linearen Funktionen zu schreiben:
f(x) = m·x
können wir jetzt genausogut schreiben:
f(x) = tan(β)·x
Da gilt: \( \textcolor{#00F}{m} = \frac{GK}{AK} = \textcolor{#00F}{tan(β)} \)