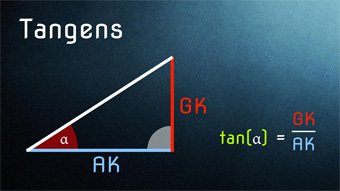
Der Tangens lässt sich über das Verhältnis von Gegenkathete zu Ankathete ausdrücken, aber auch über ein Verhältnis von Sinus zu Kosinus, wie wir im Folgenden zeigen werden.
Schauen wir uns zuerst die Definition von Sinus an:
\( \sin(β) = \frac{\text{GK}}{\text{HY}} \)
Umgestellt nach GK ergibt sich: \( \text{GK} = \sin(β) · \text{HY} \)
Die Definition für Kosinus lautet:
\( \cos(β) = \frac{\text{AK}}{\text{HY}} \)
Umgestellt nach AK ergibt sich: \( \text{AK} = \cos(β) · \text{HY} \)
Wir setzen diese beiden Formeln in die Tangensformel ein, das heißt wir ersetzen GK und AK entsprechend:
\( \tan(β) = \frac{GK}{AK} \)
\( \tan(β) = \frac{GK}{AK} \qquad | \text{ GK} = \sin(β) · HY \)
\( \tan(β) = \frac{ \sin(β) · HY }{AK} \qquad | \text{ AK} = \cos(β) · HY \)
\( \tan(β) = \frac{ \sin(β) · HY }{ \cos(β) · HY } \)
Offensichtlich können wir \( HY \) aus Zähler und Nenner des Bruches herauskürzen und es ergibt sich:
\( \tan(β) = \frac{\sin(β)}{\cos(β)} \)
Dies ist eine weitere Definition des Tangens:
Der Tangens des Winkels ergibt sich aus dem Verhältnis von Sinus des Winkels zu Kosinus des Winkels.
\( \tan(β) = \frac{\sin(β)}{\cos(β)} \)