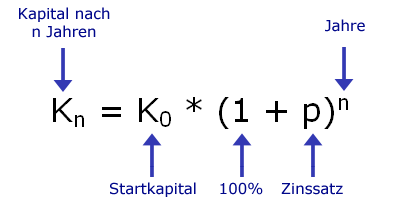
Wie wir bei gegebenem Start- und Endkapital die Jahre berechnen (also den Exponenten n, der die Laufzeit darstellt), das erfahren wir beim Rechnen mit Logarithmen.
Eine Beispielaufgabe mit Lösung:
Wie lange dauert es, um von 2 400 € auf 4 833,60 € zu kommen bei einem Zinssatz von 5 %?
Die Antwort ist: Das geht mit dem Logarithmus.
Der Rechenweg wäre mithilfe der Zinseszinsformel:
Kn = 2 400·(1+0,05)n
Kn = 4 833,60
2 400 ·1,05n = 4 833,60 | : 2 400
1,05n = 2,014
LOG anwenden:
ln 1,05n = ln 2,014
Jetzt diese Logarithmusregel anwenden: loga xy = y·loga x
ln 1,05n = ln 2,014
n · ln 1,05 = ln 2,014 | : ln 1,05
n = ln 2,014 : ln 1,05
n ≈ 14,35 Jahre
Wir wissen also, dass wir rund 14,35 Jahre benötigen, um von 2 400 € auf 4 833,60 € zu kommen.
Die Zinseszinsformel ist so wichtig, dass wir sie noch einmal aufführen: