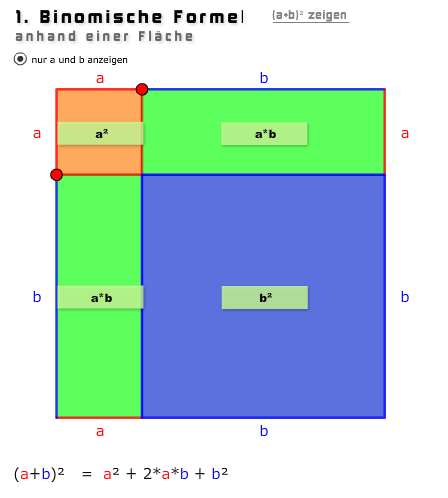
Für ein besseres Verständnis stellen wir dies nun grafisch dar. Wir starten mit der Anfangsgleichung, also 3·3 = 32, was grafisch einem Quadrat mit der Seitenlänge 3 entspricht.

Der Flächeninhalt beträgt 9.
Teilen wir jetzt die Seitenlänge auf in 3 = 2 + 1 so erhalten wir:

Wir erkennen anhand der Grafik, dass sich unsere Fläche in vier kleinere Flächen aufteilt. Das ist genau das, was wir vorhin bereits berechnet haben. Jetzt können wir erneut so vorgehen. Wir fassen die beiden grünen Flächen zusammen, da sie gleich groß sind. Wir erhalten somit für die Fläche:
Fläche = 22 + 2·(2·1) + 12 = 4 + 4 + 1 = 9
Auch hier beträgt der Flächeninhalt wieder 9. Vergleiche folgende Grafik:
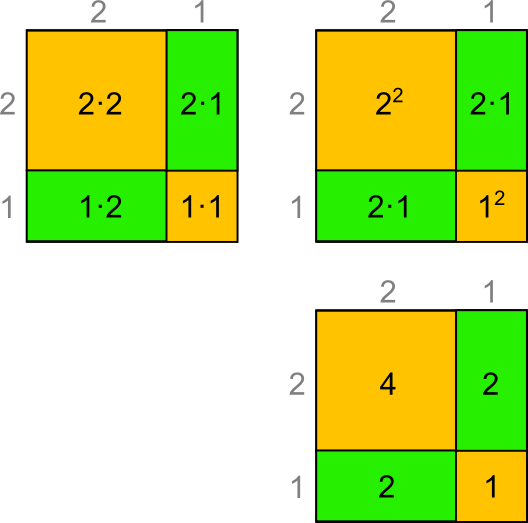
Betrachten wir unsere Rechnung allgemein und ersetzen die 2 mit einem a und die 1 mit einem b dann erhalten wir:
(2 + 1)2 = 22 + 2·(2·1) + 12
(a + b)2 = a2 + 2·(a·b) + b2
Schreiben wir das noch ohne Punkt und Komma:
(a + b)2 = a2 + 2ab + b2
Und damit haben wir unsere 1. Binomische Formel:
(a + b) · (a + b) = a2 + 2ab + b2
Hier als Grafik mit der Herleitung:
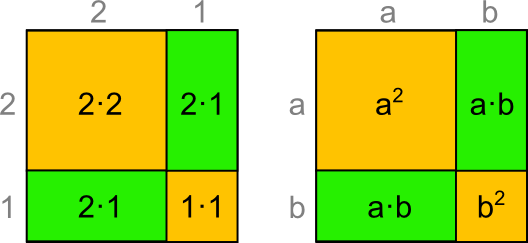
Fläche = (2 + 1) · (2 + 1)
Fläche = 2·2 + 2·1 + 1·2 + 1·1
Diese Formel formen wir weiter um:
Fläche = 2·2 + 2·1 + 1·2 + 1·1
Fläche = 2·2 + 2·1 + 2·1 + 1·1
Fläche = 2·2 + (2·1) + (2·1) + 1·1
Fläche = 2·2 + 2·(2·1) + 1·1
Fläche = 22 + 2·(2·1) + 12
Allgemein:
Fläche = a2 + 2·(a·b) + b2
Hier noch mal die Gesamtfläche (a+b)2 den vier Teilflächen gegenübergestellt (Animation):