Wir hatten uns bereits angeschaut, was eine Skizze ist und wie wir Skizzen anfertigen können.
Zur Erinnerung: Eine Skizze ist eine Zeichnung, die eine Situation grob vereinfacht darstellt und das Wesentliche zeigt. Skizzen können frei Hand gezeichnet werden oder mit Zeichenprogrammen.
Wenn wir einfache geometrische Probleme vorzuliegen haben, helfen uns Skizzen diese zu verstehen. Denn das menschliche Gehirn kann visuelle Informationen viel schneller verarbeiten als Texte.
Mit Skizzen können wir vor allem folgende geometrische Elemente darstellen:
- Punkte, Strecken, Strahlen, Geraden, Winkel
- beliebige Seiten (Längen, Breiten, Höhen) und Flächen
- Geometrische Figuren (wie Kreis, Dreieck, Viereck)
- Geometrische Körper (wie Pyramide, Kegel, Zylinder)
Beispiele von Skizzen in der Geometrie
Schauen wir uns ein paar Skizzen an, die einfache geometrische Probleme aufzeigen.
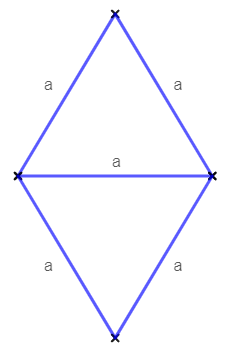
Beispiel: Gleichseitige Dreiecke
In der folgenden Skizze sehen wir zwei gleichseitige Dreiecke, die aneinander gelegt worden sind. Wir können an den Beschriftungen aller Seiten mit a erkennen, dass die Dreiecksseiten gleich lang sind. Haben wir nur einen Buchstaben wie a gegeben, dann kennen wir noch nicht den Wert, für den das a steht. Der Wert ergibt sich dann aus der Aufgabe.
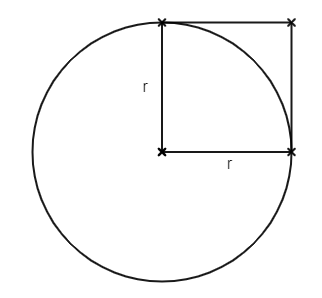
Beispiel: Kreis und Quadrat
In der folgenden Skizze sehen wir einen großen Kreis, dessen Radius eine Seite von einem Quadrat ist. Je nach Aufstellung könnten wir nun die Kreisfläche oder die Quadratsfläche berechnen.
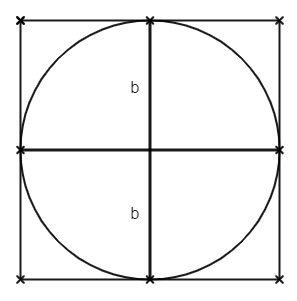
Beispiel: Quadrat umschreibt Kreis
In der folgenden Skizze sehen wir ein Quadrat, in dem sich ein Kreis befindet. Quadrat und Kreis haben den gleichen Radius, der hier mit b beschriftet wurde.
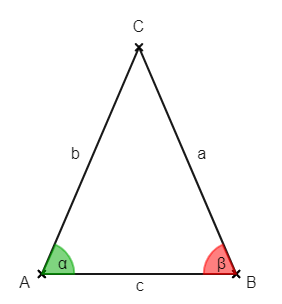
Beispiel: Dreieck mit Beschriftung
In der folgenden Skizze ist ein Dreieck eingezeichnet, und zwar mit den drei Punkten A, B, C, mit den Seiten a, b, c und den beiden Winkeln α und β.
In der Skizze ist die Dreiecksbeschriftung mit den Punkten A, B und C entgegen dem Uhrzeigersinn erfolgt. Dies wird bei geometrischen Zeichnungen fast immer so gemacht.
Wir sehen in der Skizze weiterhin, dass die Seiten, die jedem Punkt gegenüber liegen, den gleichen Namen tragen. Also beispielsweise liegt Seite a dem Punkt A gegenüber.
Zudem: Der Winkel wird direkt beim dazugehörigen Punkt eingezeichnet. Also Winkel α befindet sich direkt am Punkt A.
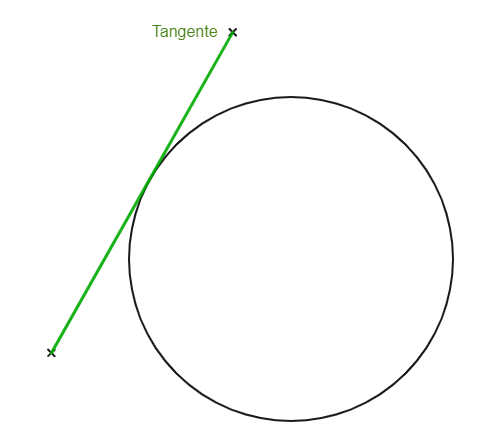
Beispiel: Tangente am Kreis
In der folgenden Skizze ist ein Kreis gezeichnet, der von einer Geraden berührt wird. Aus diesem Grund spricht man speziell von „Tangente“.
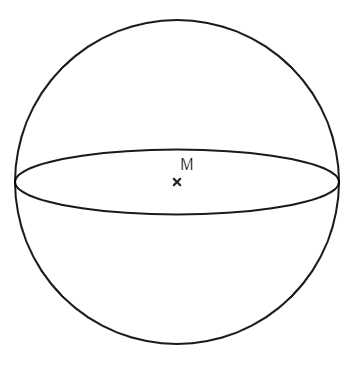
Beispiel: Kugel und Kreis
Bei dieser Skizze haben wir einen Kreis gezeichnet und weiterhin eine Ellipse in seine Mitte gezeichnet (Kreisscheibe). Dadurch sieht es so aus, als ob es eine Kugel wäre. Auch ein Punkt mit Beschriftung M wurde in die Mitte der Kugel eingetragen.
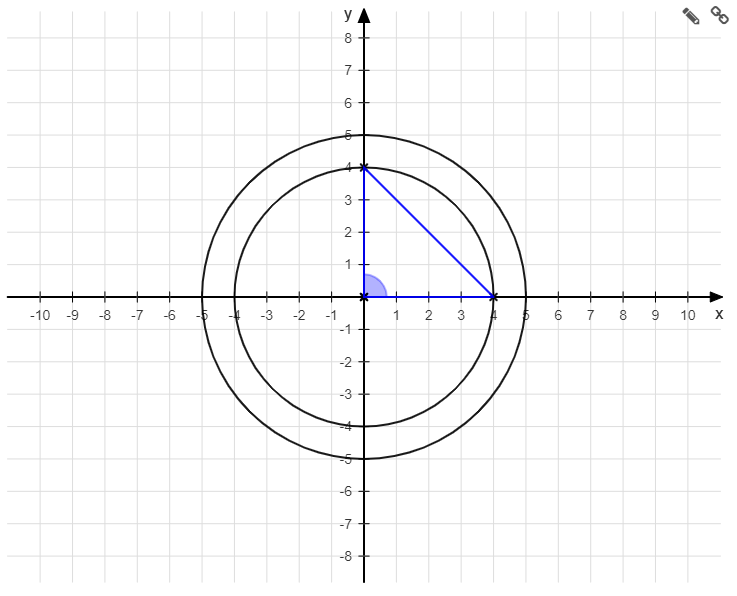
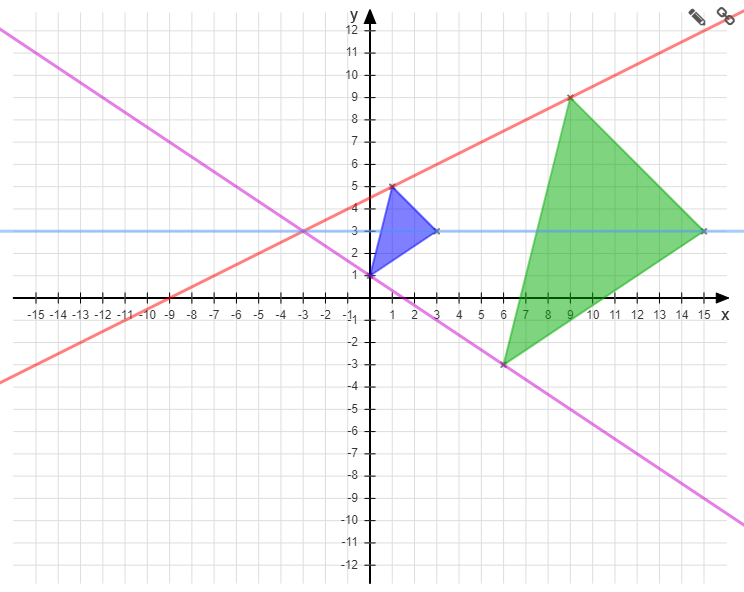
Beispiel: Kreise und Dreieck im Koordinatensystem
Wir können jederzeit auch kariertes Papier verwenden und ein Koordinatensystem zur Hilfe nehmen. Damit lassen sich Längen von Strecken wesentlich leichter ablesen.
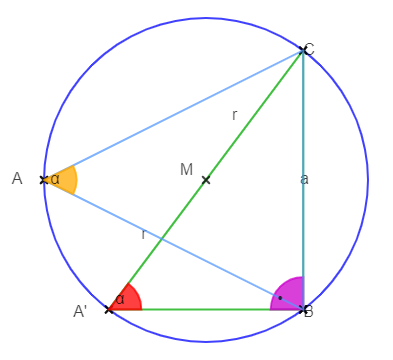
Beispiel: Dreiecke und Winkel am Kreis
Die folgende Skizze stellt einen Zusammenhang zwischen Winkeln und Seiten von Dreiecken mit Hilfe eines Kreises dar. Wir brauchen dies jetzt noch nicht verstehen. Es ist nur ein Beispiel, wie vielfältig Zusammenhänge mit Skizzen dargestellt werden können.
Beispiel: Zentrische Streckung eines Dreiecks
Diese Skizze zeigt die Vergrößerung eines Dreiecks mit Hilfe einer zentrischen Streckung.
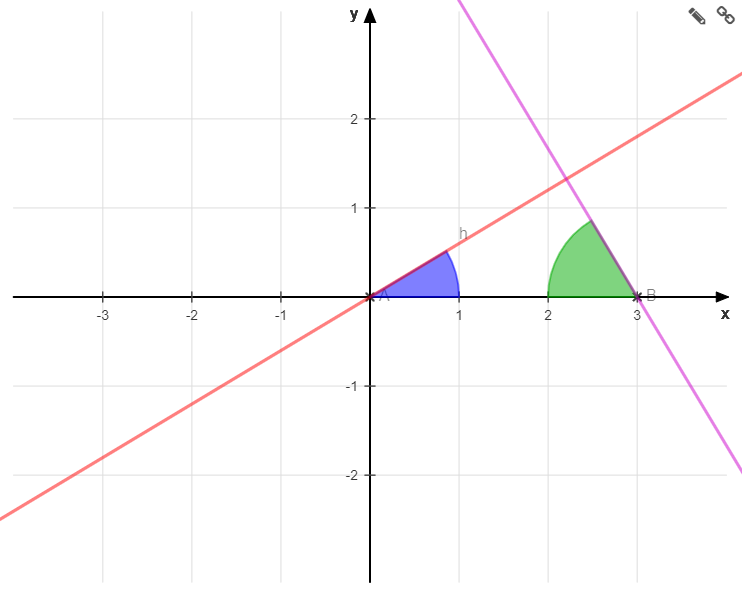
Beispiel: Winkel zwischen Geraden und x-Achse
Nachfolgend sind zwei Geraden in ein Koordinatensystem gezeichnet sowie die Winkel mit der x-Achse eingetragen. Dies können wir ebenfalls als Skizze ansehen.