Skizze anfertigen

Das Wort „Skizze“ kommt von italienisch „schizzo“, was übersetzt „Spritzer, erster Entwurf, Versuch“ heißt.

Statt Skizze können wir auch Bildentwurf, Entwurf oder Vorzeichnung sagen.

Skizzen können entweder frei mit der Hand gezeichnet werden oder wir erstellen eine Zeichnung mit entsprechender Zeichensoftware am Computer, Laptop, Smartphone oder Tablet.

Abbildung 1

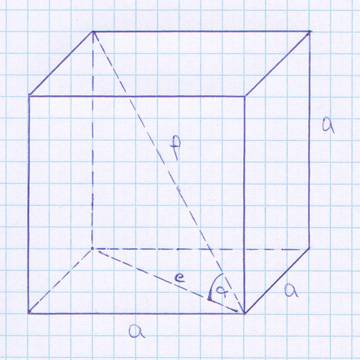
Wie gut zu erkennen ist, wurden die Strecken im Würfel mit Buchstaben beschriftet, um sie konkret benennen zu können.

Wichtig: Strecken sollten sauber mit Lineal gezeichnet werden, damit sie gerade erscheinen. Die Verwendung von kariertem Papier kann das Skizzieren ebenso erleichtern.

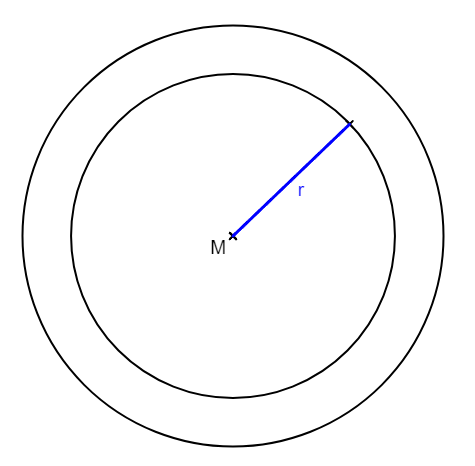
Eine mit Zeichensoftware am Computer erstellte Skizze könnte so aussehen (zum Beispiel Fläche eines runden Gartenbeets):

Elemente von Skizzen

Mit Skizzen können wir folgende Elemente darstellen:

• Punkte, Strecken, Strahlen, Geraden, Winkel
• beliebige Seiten (Längen, Breiten, Höhen)
• Flächen in verschiedenen Formen
• Geometrische Figuren (wie Kreis, Dreieck, Viereck)
• Geometrische Körper (wie Pyramide, Kegel, Zylinder)
• Graphen von Funktionen
• Diagramme (wie Kreisdiagramme, Streifendiagramme, Baumdiagramme)

Maßstabsgetreue Skizzen

Skizzen können „maßstabsgetreu“ sein, das heißt, alle Längen der Seiten in der Skizze stimmen mit allen Längen im Original überein (im Maßstab).

Als Beispiel: Zwei gezeichnete Wände eines Zimmers sind in der Skizze 5 cm und 10 cm lang. Im Original (ohne Verkleinerung) sind die Wände 5 m und 10 m lang. Die Wände wurden maßstabsgetreu gezeichnet, also im gleichen Größenverhältnis zueinander.

Im Gegensatz dazu gibt es nicht maßstabsgetreue Skizzen. Hier unterscheiden sich die Längen der gezeichneten Seiten. Sie weichen von der Realität bzw. den Werten in der Aufgabe ab. Meist geht es bei diesen Skizzen nur darum zu zeigen, wie die Situation grob aussieht und wie Figuren/Körper angeordnet und beschriftet sind.

Beispiele für Skizzen (Alltag)

Viele Situationen im Alltag lassen sich als Skizze darstellen. Nachfolgend ein paar Beispiele:

• Höhen von Bergen, Gebäuden, Türmen, Menschen, Bäumen, Leitern, Gegenständen
• Struktur bzw. Anordnung von Landschaften, Feldern, Gärten, Wohnflächen etc.
• Verbindung von geometrischen Körpern (z. B. Kugel innerhalb von Würfel)
• Winkel von Geräten, Höhenwinkel, Winkel bei Vermessungen von Landschaften und Dächern
• Massen auf Waagen darstellen
• Würfelexperimente zeichnen
• Mengen darstellen (z. B. Anzahl rote, grüne, blaue Flaschen)
• und viele mehr.

Schritte zum Anfertigen von Skizzen

Zum Anfertigen einer Skizze müssen wir zuerst verstehen, was uns in der Aufgabe gegeben ist. Die gegebenen Objekte müssen wir erkennen und können sie dann im Zusammenhang als Skizze zeichnen.

Die Schritte zum Anfertigen einer Skizze sind:

1. Objekte in der Aufgabe erkennen
2. Objekte in Zusammenhang bringen
3. Objekte im richtigen Zusammenhang skizzieren

Beispiel: Skizze zu einer Alltagssituation

Erstellen wir eine Skizze anhand folgender Aufgabe:

Ein Bauland mit rechteckiger Grundstücksfläche soll in 10 gleich große Quadratsflächen aufgeteilt werden. Diese Teilflächen sollen an verschiedene Eigentümer verkauft werden. Das Grundstück hat eine Abmessung von 400 m mal 1000 m. Wie groß ist jede Quadratsfläche?

1. Objekte in der Aufgabe erkennen:

   Rechteck (geteilt in 10 Quadrate)

2. Objekte in Zusammenhang bringen:

   Die 10 Quadrate ergeben das Rechteck.

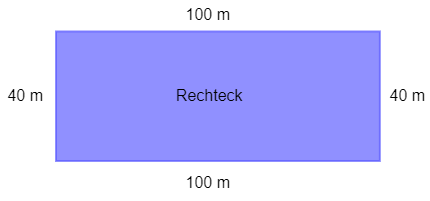
3. Objekte im richtigen Zusammenhang skizzieren:

Wir müssen beim Zeichnen der Skizze beachten, dass die 100 m Seite länger ist als die 40 m Seite, sodass eine passende Form der Rechtecksfläche entsteht. Das Lineal hilft uns hier weiter: Wir können die 100 m als 10 cm auf Papier zeichnen und die 40 m als 4 cm.

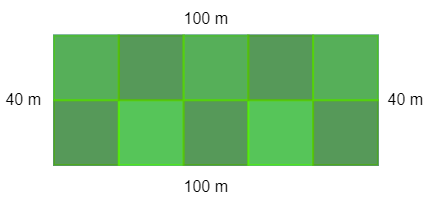
Nachdem wir das Rechteck gezeichnet haben, können wir die 10 gleich großen Quadrate einzeichnen:

Erkenntnis:

Wir sehen anhand der Skizze, dass die Quadrate nur auf diese eine Art angeordnet werden können: Als zwei Reihen mit jeweils 5 Quadratsfeldern. Außerdem bekommen wir eine Vorstellung davon, wie groß eine Quadratsfläche etwa sein kann.

Lösung der Aufgabe:

Die Rechtecksfläche ergibt sich, wenn wir beide gegebenen Seiten miteinander multiplizieren:

Rechtecksfläche = 40 m · 100 m
Rechtecksfläche = 4000 m²

Eine Quadratsfläche erhalten wir, wenn wir die Rechtecksfläche :10 dividieren:

Quadratsfläche = Rechtecksfläche : 10
Quadratsfläche = 4000 m² : 10
Quadratsfläche = 400 m²

Mit Blick auf die Skizze wissen wir, dass die Rechtecksseite mit 40 m in zwei Teile zerlegt wird, also 40 m : 2 = 20 m.

Und dass die Rechtecksseite mit 100 m in 5 Teile zerlegt wird, also 100 m : 5 = 20 m.

Folglich ergibt sich die Antwort:

Jede Quadratsfläche hat eine Fläche von 400 m². Die Quadrate sind 20 m · 20 m groß.

Arten von Skizzen

Es gibt verschiedene Arten von Skizzen in der Mathematik, so zum Beispiel:

1. Situationsskizze: Diese Skizze stellt die Situation stark vereinfacht dar. Man erkennt aber Aufbau und Zusammenhänge.

2. Ideenskizze (Entwurfsskizze): Diese Skizze hilft, eine Idee grafisch darzustellen und zu erläutern.

3. Planskizze (Planfigur): Diese Skizze wird erstellt bevor eine geometrische Konstruktion ausgeführt wird. Ziel ist es zu erkennen, alle wichtigen Informationen zu zeigen (z. B. welche Strecken und Winkel vorliegen).

4. Fertigungsskizze: Dies ist eine technische Skizze, sie stellt Gegenstände zum Zweck ihrer Herstellung dar.

Nicht nur in der Mathematik, sondern auch in der Kunst gibt es verschiedene Skizzen. Hier sind es zum Beispiel: Croquis (sehr schnelle Zeichnung), Porchade (Skizze mit Farben, um Szene einzufangen), Portrait-Skizze (Zeichnung des Gesichts), analytische Skizze (die Einzelteile sind erkennbar, um eine Struktur zu verstehen), perspektivische Skizze (Zeichnung von dreidimensionalen Szenen), Stillleben-Skizze (schnelle Abbildung einer Szene), Landschaftsskizze (Szenen aus der Natur), urbane Skizze (Zeichnung des Stadtlebens), Körperstudie/Akt (Zeichnung von menschlichen Körpern), emotionale Skizze (Zeichnung von Gefühlen).