Eine Gerade ist eine gerade Linie, die wir ins Koordinatensystem einzeichnen. Sie wird durch eine Funktionsgleichung wie zum Beispiel f(x) = 2·x beschrieben.
Zwei Geraden können sich in einem, keinem oder mehreren Punkten schneiden. Im Folgenden betrachten wir diese Fälle.
Wie bereits bekannt ist, ist die Normalform einer linearen Funktion anzugeben als:
f(x) = m·x + n
Wenn wir nun zwei lineare Funktionen haben, können wir die Lage beider Geraden zueinander untersuchen.
Es ergeben sich drei Fälle:
- Genau einen Schnittpunkt
- Keinen Schnittpunkt
- Unendlich viele Schnittpunkte
Schauen wir uns die Fälle genauer an.
Lösungsmöglichkeiten
Haben wir zwei Geraden und sind an ihrer Lage zueinander interessiert, so müssen wir die Funktionsgleichungen gleichgesetzen.
Gleichsetzen heißt, wir müssen sie in Form einer Gleichung nebeneinander schreiben: f(x) = g(x). Lösen wir die sich daraus ergebende Gleichung, können mehrere Fälle für die Lösung auftreten:
1. Es kommt genau eine Lösung heraus. → Wir haben genau einen Schnittpunkt.
2. Die Gleichung ist unwahr. Keine Lösung. → Wir haben keinen Schnittpunkt. Die Geraden sind parallel.
3. Die Gleichung ist immer wahr. Unendlich viele Lösungen. → Die Geraden liegen aufeinander (sie sind identisch).
Veranschaulichung am Graphen
In der folgenden Abbildung sind alle Lösungsmöglichkeiten mit Beispielen von Funktionsgraphen zu sehen.
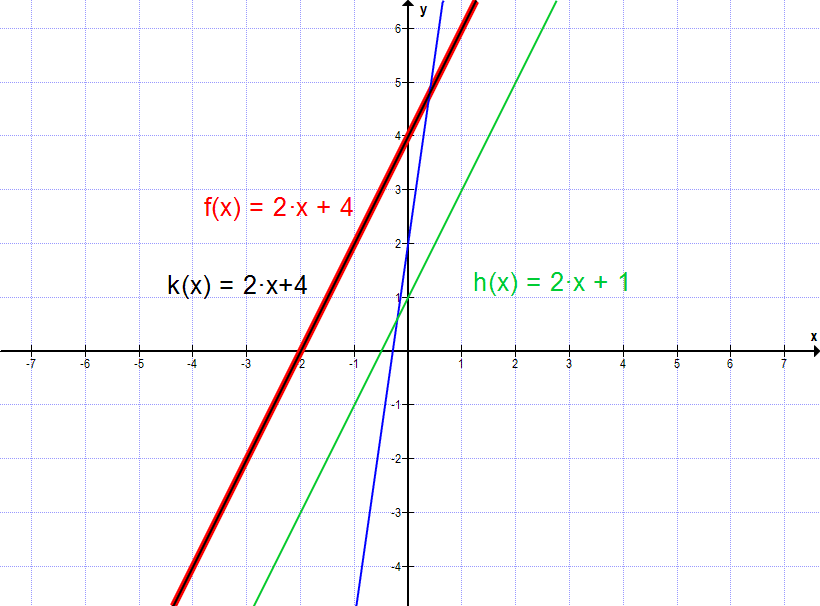
g(x) = 7·x + 2 und h(x) = 2·x + 1 haben einen Schnittpunkt
f(x) = 2·x + 4 und h(x) = 2·x + 1 haben keinen Schnittpunkt
f(x) = 2·x + 4 und k(x) = 2·x + 4 haben unendlich viele Schnittpunkte.
Schauen wir uns als nächstes an, wie wir Schnittpunkte rechnerisch bestimmen können.