Zum Nachweis, dass zwei Geraden senkrecht zueinander stehen (orthogonal sind) haben wir diese Formel verwendet: mf · mg = -1
In Worten ausgedrückt: Wir müssen beide Steigungen multiplizieren und es muss -1 herauskommen, dann sind die Geraden senkrecht zueinander. Dass das gilt, können wir auf verschiedene Arten nachweisen.
Zwei Beweise seien im Folgenden vorgestellt:
Beweis 1
Mit Hilfe des Höhensatzes von Euklid können wir den Nachweis führen. Der Höhensatz lautet h² = p · q.
Schauen wir uns im Folgenden eine Dreiecksgrafik an, bei der die Höhe h und die Teilstrecken p und q eingetragen sind. Dabei haben wir das rechtwinklige Dreieck gedreht, was keine Auswirkungen auf den Höhensatz hat:
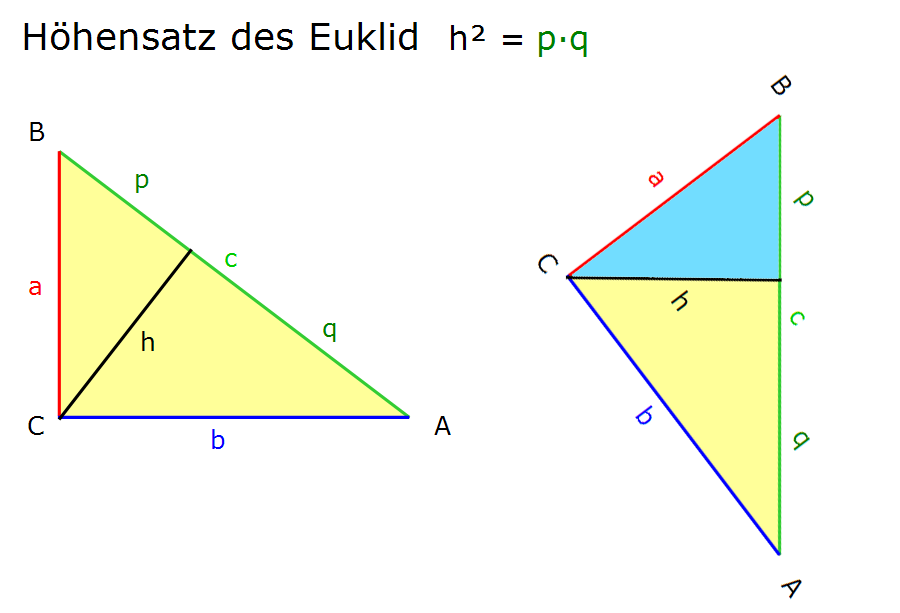
Wenn wir uns die beiden Teildreiecke anschauen, so können wir diese als zwei Steigungsdreiecke interpretieren.
Legen wir das Dreieck an den Schnittpunkt von zwei sich schneidenden Geraden:
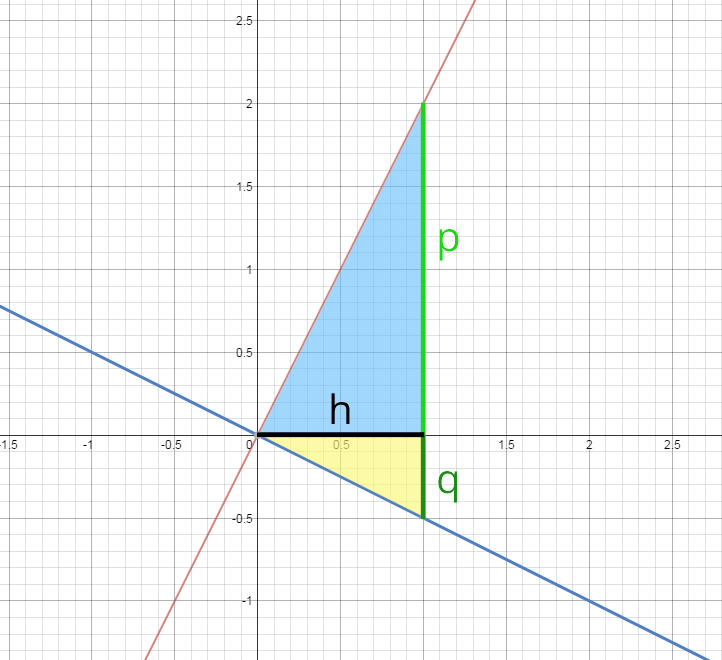
Wenn wir ein Steigungsdreieck haben, so wird oft der Teil auf der x-Achse mit 1 gewählt (unsere Strecke h in der Grafik).
Tun wir das auch hier (dieser gewählte Fall hat keinen Einfluss auf den Gesamtbeweis, er gilt auch für andere Fälle, man sagt übrigens dazu „ohne Beschränkung der Allgemeinheit“). Setzen wir also h = 1. Dann entsprechen p und q direkt unseren Steigungen, die nach oben oder unten abgetragen werden: mf und mg.
Da mg nach unten orientiert ist, versehen wir es mit einem negativen Vorzeichen. An dieser Stelle kann man sich merken, dass eine um 90° gedrehte Gerade stets einen Vorzeichenwechsel erfährt, daher werden mf und mg immer Plus- und Minus-Vorzeichen haben. Wir können festhalten:
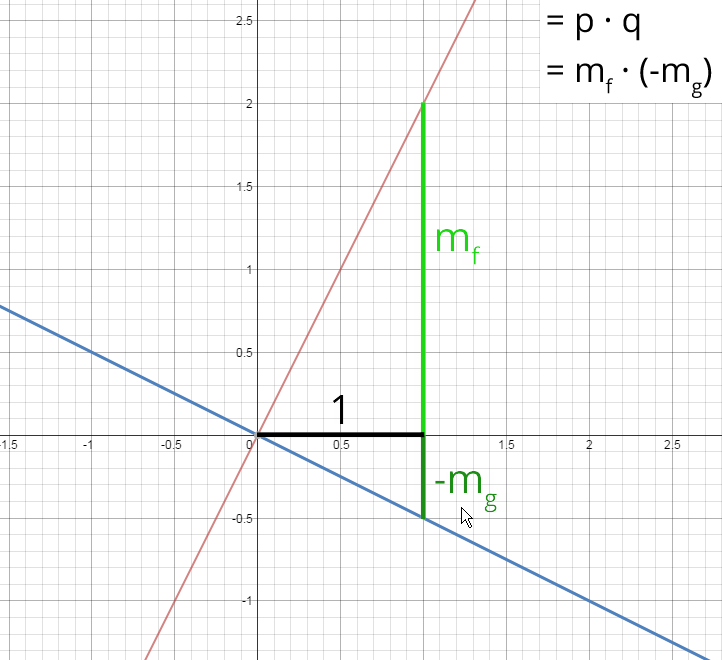
Stellen wir den Höhensatz auf:
h² = p · q | p = mf und q = -mg
h² = mf · (-mg)
(1)² = mf · (-mg)
1 = mf · (-mg)
Das können wir noch umformen, indem wir durch -1 dividieren, wir erhalten: -1 = mf · mg, was genau der verwendeten Bedingung für Orthogonalität entspricht.
Beweis 2
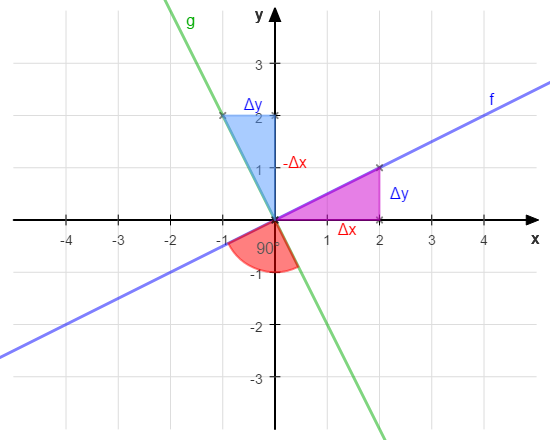
Haben wir eine beliebige Gerade f (blau), so können wir die Steigung dieser Geraden mit \( m_f = \frac{\textcolor{blue}{\triangle y}}{\textcolor{red}{\triangle x}} \) angeben (Steigungsdreieck).
Wenn wir nun diese Gerade nehmen und um 90° drehen, so können wir wiederum ein Steigungsdreieck einzeichnen.
Es fällt auf, dass sich hier gerade \(\textcolor{red}{\triangle x}\) und \(\textcolor{blue}{\triangle y}\) vertauschen (dreht diese mit um 90°). Zudem ändert das Steigungsdreieck seine Richtung und damit die Steigung ihr Vorzeichen. Die neue Gerade g (grün) hat also die Steigung \(m_g = -\frac{\textcolor{red}{\triangle x}}{\textcolor{blue}{\triangle y}}\).
Wenn wir nun beide Steigungen durch Multiplikation in Beziehung bringen, so erhalten wir:
\( m_f · m_g = \frac{ \textcolor{red}{\triangle x} }{ \textcolor{blue}{\triangle y} } · \left(-\frac{ \textcolor{blue}{\triangle y} }{ \textcolor{red}{\triangle x} }\right) = -1 \)
Dies ist der zweite Nachweis für die Orthogonalitätsbedingung bei Geraden.
Nun haben wir zwei Beweise kennengelernt, die zeigen, dass wir die die Orthogonalität mit Hilfe der Formel mg · mf = -1 überprüfen dürfen.