Wenn wir einen bestimmten Punkt auf einem Graphen untersuchen möchten, so müssen wir klar machen, von welchem Punkt wir sprechen.
Zur Orientierung nehmen wir uns daher die beiden Achsen (x- und y-Achse) des Koordinatensystems und ordnen dem Punkt zwei Werte zu. Der Punkt hat damit zwei Koordinaten und wir schreiben P(x|y), wobei wir für x und y Zahlen eintragen. Damit ist die Position des Punktes eindeutig bestimmt.
Manchmal wird die waagerechte Achse als „Breite“ und die senkrechte Achse als „Höhe“ bezeichnet. Meistens wird die waagerechte Achse mit der Variablen x bezeichnet und die senkrechte Achse mit y. Je nach Situation kann man aber auch andere Variablen verwenden. So wird bei Zeitangaben auch der Buchstabe t statt x verwendet.
Bestimmen wir als nächstes einen Punkt, der sich auf einem Graphen befindet.
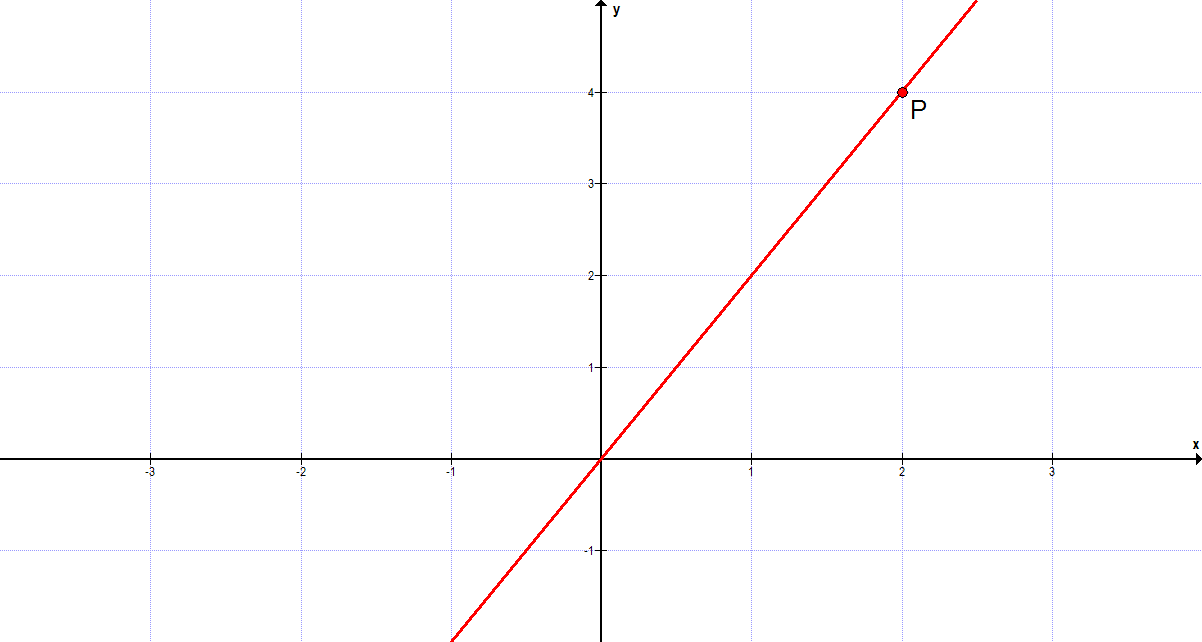
Damit jeder weiß, von welchem Punkt die Rede ist, müssen wir seine Position also angeben.
Dazu schauen wir uns an, wie weit der Punkt vom Koordinatenursprung (also dort, wo sich x- und y-Achse schneiden) entfernt ist.
Gehen wir vom Koordiantenursprung so weit nach rechts (liegt der Punkt links, dann nach links), wie der Punkt entfernt ist. Sind wir genau „unterhalb“ dem gesuchten Punkt, haben wir die „Breite“ gefunden (also den x-Wert).
Die Höhe finden wir, wenn wir nun nach oben gehen, bis wir die Höhe des Punktes erreichen. Die Höhe kann anhand der senkrechten Achse abgelesen werden. Der Punkt wird also mit P(Breite|Höhe) angegeben, was in unserem Beispiel P(2|4) ist.
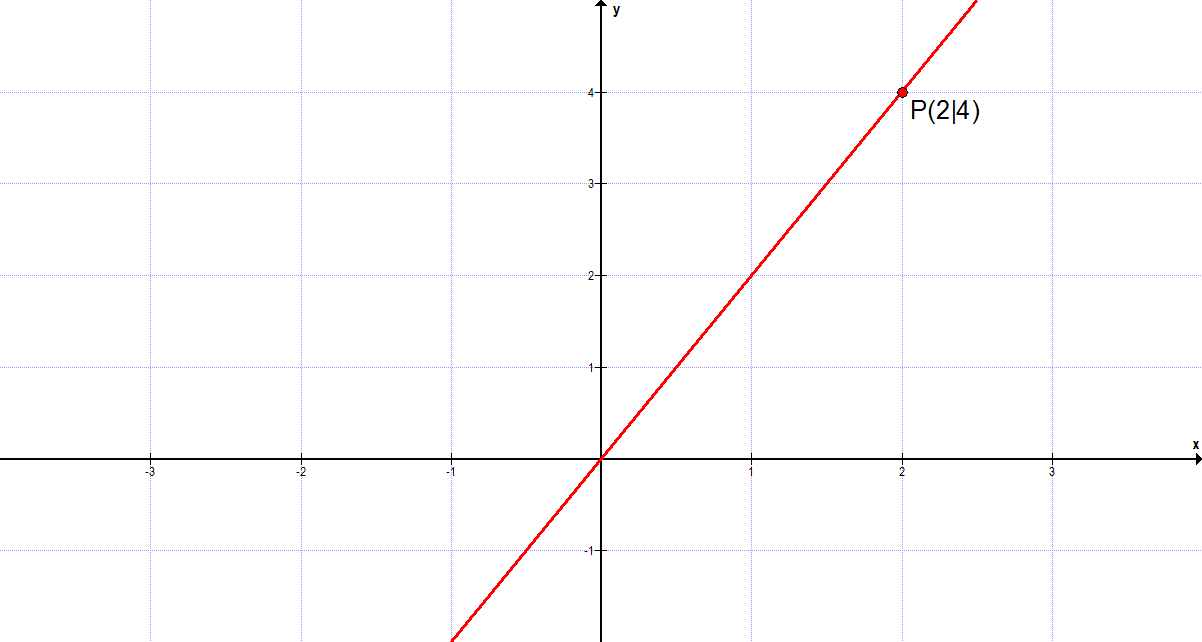
Der Punkt P(2|4) befindet sich also auf dem eingezeichneten Graphen.