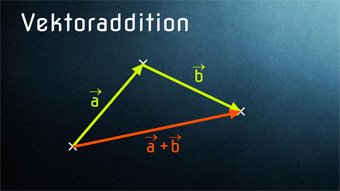
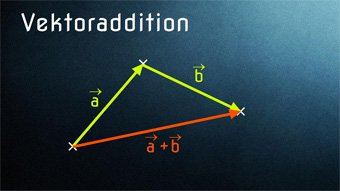
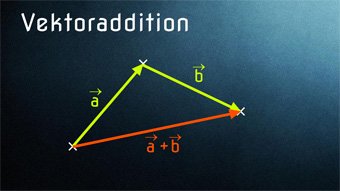
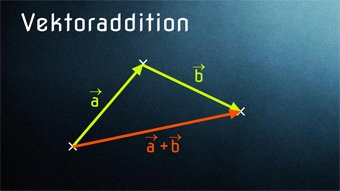
Lektion VEK03: Vektoraddition - Matheretter
In diesen Mathe-Videos zeigen wir euch, wie die Vektoraddition funktioniert, rechnerisch und geometrisch.
Matheretter
Lektion VEK03: Vektoraddition
Inhalte:
- Wie addiert man einen Ortsvektor mit einem Verschiebungsvektor?
- Was ist die komponentenweise Addition?
- Wie addiert man zwei Ortsvektoren miteinander?
- Was ist die Spitze-Fuß-Regel?
- Wie verläuft die Addition von mehreren Vektoren?
- Was ist eine geschlossene Vektorkette?
Voraussetzung:
Laut Lehrplan: 7. - 8. Klasse
Das Wissen zur Vektor-Einführung und zum Bestimmen von Vektoren können wir nun nutzen, um Vektoren zu addieren.
Wie das genau funktioniert, schauen wir uns in den Videos rechnerisch und geometrisch an. Wir lernen auch Rechenregeln wie zum Beispiel das Kommutativgesetz der Vektoraddition kennen.
Weitere Videos für Kunden:
-
VEK03-1 Vektoraddition - Addition von Orts- und VerschiebungsvektorEinführung der Addition über Ortsvektoren und Verschiebungsvektoren. Komponentenweise Addition. Geometrische Darstellung für Ortsvektor a + Verschiebungsvektor v = Ortsvektor b
-
VEK03-2 Vektoraddition - Addition von 2 OrtsvektorenWie addiert man zwei Ortsvektoren. Regel für die geometrische Darstellung: Verschiebung der Vektoren (Anfangspunkt auf Endpunkt, Spitze-Fuß-Regel). Kommutativgesetz für Vektoren a + b = b + a. Resultierender Vektor als kürzeste Verbindung (Vektorbeträge).
-
VEK03-3 Vektoraddition - Addition mehrerer VektorenWie addiert man mehrere Vektoren miteinander. Die Komponenten aller Vektoren müssen addiert werden. Schrittweise geometrische Darstellung der Vektoraddition auf der Ebene.
-
VEK03-4 Vektoraddition - Beispiel zur Addition, Nullvektor, VektorketteGeometrisches Beispiel einer Vektoraddition, Verschiebung der Vektoren aufeinander, Kommutativgesetz geometrisch, Nullvektor bei der Addition, geschlossene Vektorkette, Darstellung der Komponenten eines Vektors als Vektoren.
Nachstehend die Vektorprogramme aus den Videos:
-
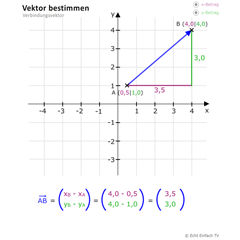Vektor bestimmenDieses Programm berechnet die Komponenten eines Vektors aus den Koordinaten der zwei Punkte A und B. Ist der Anfangspunkt im Koordinatenursprung, so spricht man vom Ortsvektor. -
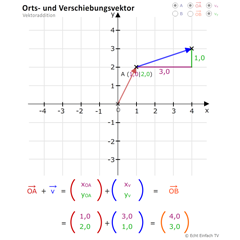Vektoraddition: Orts- und VerschiebungsvektorMit diesem Programm können Orts- und Verschiebungsvektor miteinander addiert werden. Die x- und y-Komponenten werden angezeigt sowie der resultierende Vektor. -
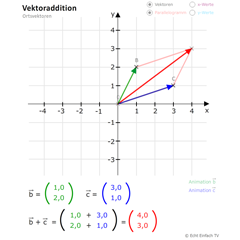Vektoraddition: OrtsvektorenHier können zwei Ortsvektoren miteinander addiert werden, geometrisch entspricht das einer Verschiebung des einen Vektors auf den anderen. Dies kann als Animation und als Parallelogramm dargestellt werden. -
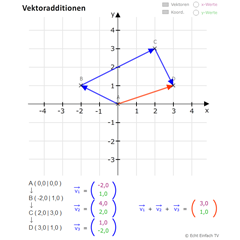VektoradditionenDieses Programm erlaubt die Addition von 3 Vektoren. Die Vektoren ergeben sich aus Punkten. Der resultierende Vektor wird rot dargestellt. -
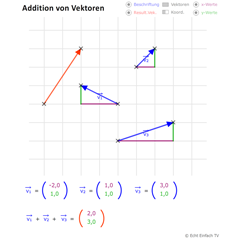Addition von Vektoren (Verbindungsvektoren)Mit Hilfe dieses Programms können Vektoren beliebig festgelegt und frei auf der Ebene verschoben werden. Beim korrekten Anordnen der Vektoren ergibt sich der resultierende Vektor.
Hier findest du 2 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 2 Lernchecks, mit denen du dein Wissen testen kannst.
Häufige Fragen:
- Einfache Vektoraddition: Welchen Winkel schließt der Summenvektor c=a+b mit der x-Achse ein?
- Grafische Addition von Vektoren überprüfen
- Vektoren addieren - grafisch darstellen
- Vektoraddition. Die Vektoren s,r und t im Dreieck sind gegeben
- Kann man Zahl + Vektor weiter zusammenfassen: 5 + [3 , 2 , 7]
Finde weitere Fragen und Antworten in der Mathelounge.