Wir kennen bereits die Polynomfunktionen mit Funktionstermen wie x, x², x²+2, x³ + x + 1 usw. Also namentlich lineare Funktionen, quadratische Funktionen, kubische Funktionen etc.
Als nächstes lernen wir einen weiteren Typ kennen, und zwar die Exponentialfunktionen. Mit deren Hilfe lassen sich Wachstums- und Zerfallsprozesse in der Natur beschreiben.
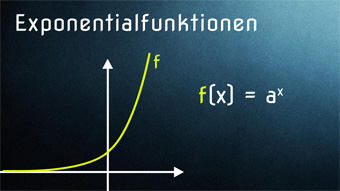
Es handelt sich um eine Exponentialfunktion, wenn sich die Unbekannte x im Exponenten befindet. Beispiel: f(x) = 2x
Weitere Beispiele:
f(x) = 3x
g(x) = 5x
h(x) = 100x
Dabei ist der Wert der Basis festgelegt (ein konstanter Wert).
Die allgemeine Form der Exponentialfunktion lautet: f(x) = ax
Und es gilt x ∈ ℝ, wobei a konstant und positiv ist, außerdem a ≠ 0 (da 00 problematisch ist).
Das a muss stets positiv sein. Denn wenn a negativ wäre, dann würden wir beispielsweise erhalten:
\( (-2)^{ \frac{1}{2} } = \sqrt{-2} = \text{nicht definiert} \)
Interaktiver Graph
Einfach den Punkt nach oben und unten bewegen. Er gibt den Wert der Basis a an: