Wir stellen die kubische Gleichung als Linearfaktoren da. Die Darstellung mit Linearfaktoren einer kubischen Gleichung sieht so aus:
(x - x1) · (x - x2) · (x - x3)
Die Linearfaktoren können wir auch bei unserer berechneten Lösung darstellen:
(x3 + 6·x2 +11·x +6) =(x + 1) · (x2 + 5·x +6) = (x + 1) · (x + 2) · (x + 3)
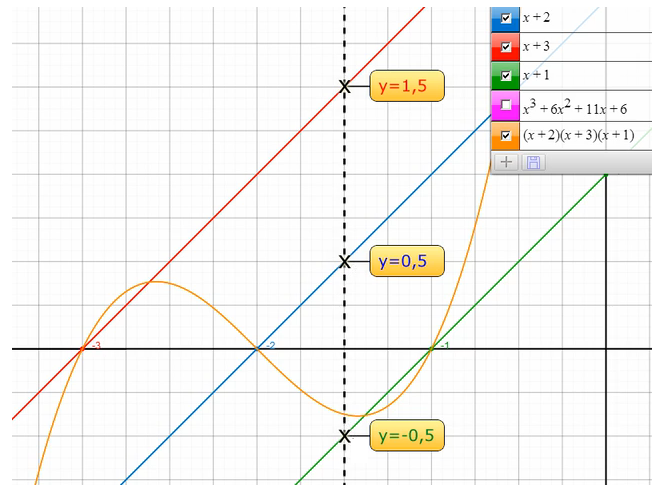
Betrachten wir, wie das Polynom als Graph aussieht. Auch die einzelnen Linearfaktoren stellen wir als lineare Funktionen da:
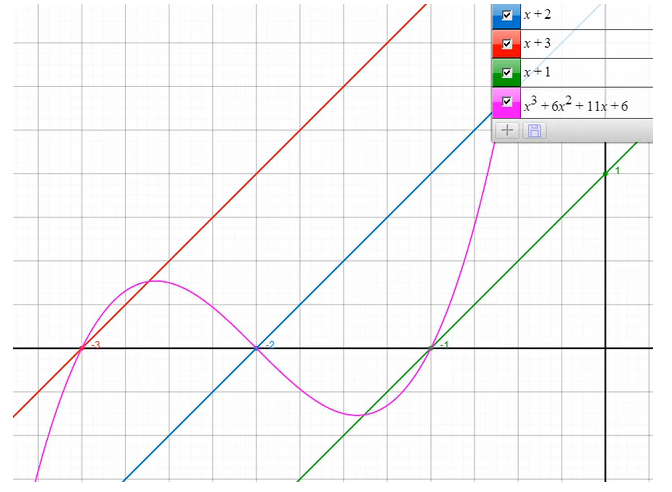
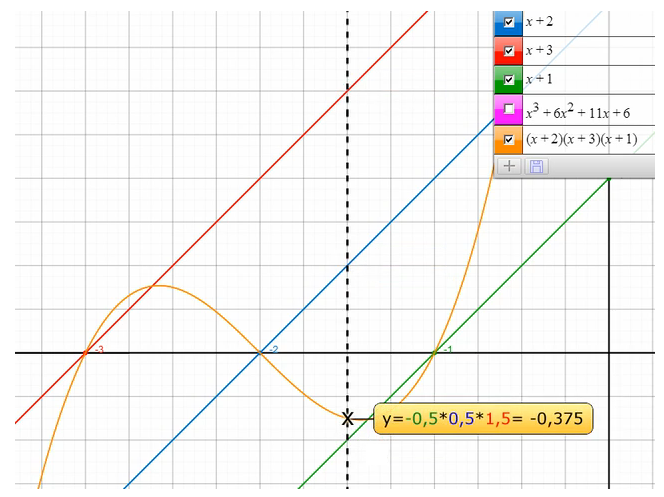
Wir sehen, dass die Nullstellen der einzelnen Geraden, die die Linearfaktoren darstellen sollen, die selben Nullstellen sind, die unser Polynom besitzt. Wir können die Gleichung in diesem Fall auch durch Ablesen der Nullstellen des Graphens lösen. Das Polynom nimmt den Wert an der Stelle x an, der dem Produkt der Werte der drei Geraden an der Stelle x entspricht.
Das sehen wir anhand der nächsten beiden Grafiken: