Bestimmt man die Lösung einer kubischen Gleichung, so berechnet man die Nullstellen einer Funktion 3. Grades. Diese Funktion sieht allgemein so aus:
f(x) = x³ + r·x² + s·x + t
Um solche Gleichungen zu lösen, stehen mehrere Lösungsverfahren zur Verfügung:
- Cardanische Formeln
Kubische Gleichungen haben in den reellen Zahlen mindestens eine und maximal drei Lösungen. Sie können also 1, 2 oder 3 Lösungen haben.
Warum eine kubische Gleichung mindestens eine Lösung hat, machen wir uns klar, indem wir eine beliebige kubische Gleichung als Funktion mit Graphen betrachten:
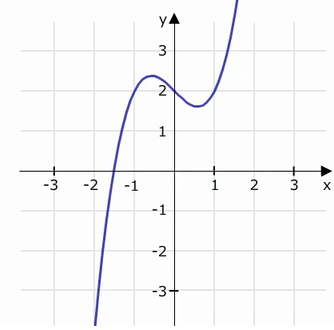
Alle Gleichungen 3. Grades haben diese oder eine ähnlich verlaufende Form des Graphen. Wenn wir x gegen unendlich laufen lassen, gehen auch die Funktionswerte (y) gegen unendlich.
Wenn wir x gegen minus unendlich laufen lassen, gehen auch die Funktionswerte (y) gegen unendlich.
Wenn die Werte von minus unendlich zu plus unendlich laufen (oder umgekehrt) und die Funktion stetig ist (also keine Definitionslücken hat, was bei kubischen Gleichungen gegeben ist), sehen wir, dass die Funktion mindestens einmal durch die x-Achse verlaufen muss. Die Funktion hat also mindestens eine Nullstelle.
Damit ist klar, dass jede kubische Funktion mindestens eine Lösung haben muss.
Wer sich das nochmal genauer anschauen möchte, kann mit diesem Rechner einige kubische Gleichungen erstellen und sehen, dass die Gleichung mindestens eine Lösung hat.

