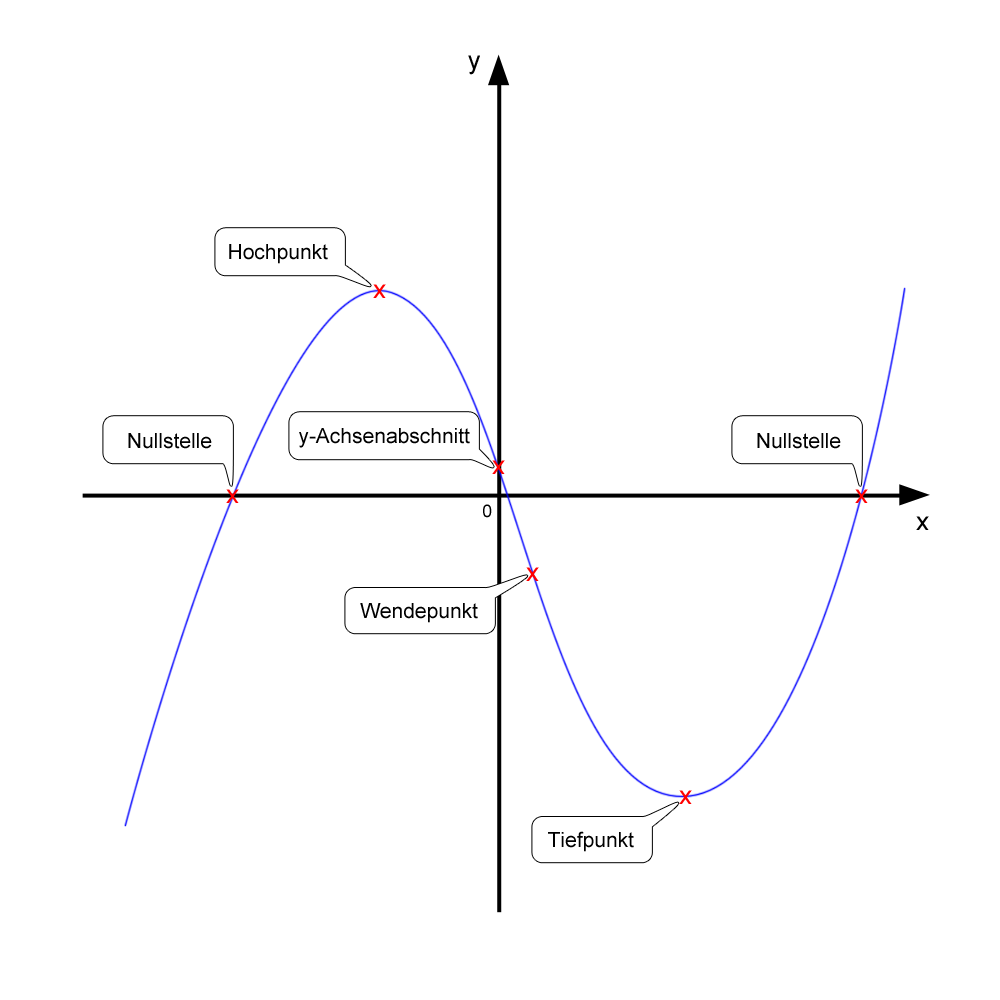
Bei einer Kurvendiskussion versuchen wir, wesentliche Eigenschaften einer Funktion zu ermitteln. Dazu gehören Nullstellen, y-Achsenabschnitt, Hochpunkte und Tiefpunkte sowie Wendepunkte. Hierzu verwenden wir u. a. die Nullstellenberechnung und die Differentialrechnung.
Eine wahrscheinlich treffendere Beschreibung für „Kurvendiskussion“ wäre „Funktionsuntersuchung“, da wir die Funktion auf Besonderheiten untersuchen.
Schauen wir uns nachfolgend allgemein die Untersuchungen an, die wir bei einer Kurvendiskussion durchführen müssen.
1. Definitionsmenge
Bei Funktionen stellt sich die Frage, ob für die Funktion f(x) = y für jeden Wert von x auch ein Wert von y entstehen kann, ohne dass ein „nicht definiert“ erscheint.
Wenn wir die Definitionsmenge festlegen, beantworten wir also die Frage: „Was dürfen wir für x einsetzen?“
Beispiel: Lineare Funktion mit Gleichung f(x) = 3·x + 5.
Hier haben wir kein Problem. Egal, welchen Wert wir für x einsetzen, wir erhalten stets einen gültigen y-Wert.
2. Symmetrie
Eine Aussage über die Symmetrie einer Funktion (Polynomfunktion) lässt sich treffen, indem wir die Exponenten der Funktionsgleichung betrachten.
Achsensymmetrie
Sind alle Exponenten gerade, dann liegt Achsensymmetrie vor.
Beispiele: f(x) = x2 oder f(x) = 3·x4 + 5·x2.
~plot~ x^2;3*x^4+5*x^2;[[5]];noinput ~plot~
Hinweis: Sollten wir eine Funktionsgleichung wie f(x) = x2 + 3·x0 haben, so gilt auch hier, dass die Funktion achsensymmetrisch ist, da der Exponent 0 bei x0 gerade ist.
Punktsymmetrie
Sind alle Exponenten ungerade, dann liegt Punktsymmetrie zum Koordinatenursprung vor.
Beispiele: f(x) = x3 oder f(x) = 7·x3 + x1.
~plot~ x^3;7*x^3+x;[[4]];noinput ~plot~
Sind gerade und ungerade Exponenten in der Funktionsgleichung vorhanden, so liegt keine Punktsymmetrie zum Koordinatenursprung vor. Auch liegt dann keine Achsensymmetrie vor.
3. Verhalten im Unendlichen
Beim Verhalten im Unendlichen (siehe Grenzwerte) treffen wir eine Aussage, ob die Funktionswerte (also y-Werte) für x gegen plus Unendlich fallen oder steigen (x → +∞). Genauso prüfen wir, ob die Funktionswerte für x gegen minus Unendlich fallen oder steigen (x → -∞).
Wir können dies mit der Limes-Schreibweise notieren.
Zum Beispiel: \( \lim \limits_{x \to -\infty} x^2 = +\infty \) und \( \lim \limits_{x \to +\infty} x^2 = +\infty \)
Wenn wir die Limes-Schreibweise noch nicht kennen, können wir stattdessen notieren:
„Verhalten von x gegen +∞ → Funktionswerte steigen“ (oder fallen, je nach Funktion)
„Verhalten von x gegen -∞ → Funktionswerte steigen“ (oder fallen, je nach Funktion)
4. Stetigkeit/Unstetigkeit
Eine stetige Funktion erkennen wir daran, dass ihr Graph in einem Koordinatensystem eine zusammenhängende Kurve ergibt. Das heißt, der Graph hat keine Sprünge (wie bei bspw. vorkommenden Definitionslücken oder Sprungfunktionen der Fall). Einfach gesagt: Wir können den Graphen ohne Absetzen des Stiftes zeichnen.
Beispiele:
f(x) = x4 ist stetig. Jedoch ist g(x) = \( \frac{1}{x} \) nicht stetig.
~plot~ x^4;1/x;[[4]];noinput ~plot~
5. Nullstellen
Wir ermitteln die Stellen, an denen der Graph die x-Achse schneidet. Hierzu müssen wir die Funktionsgleichung null setzen und nach x auflösen.
Kurz: \( x_N \) ist Nullstelle. Demnach \( f(x_N) = 0 \).
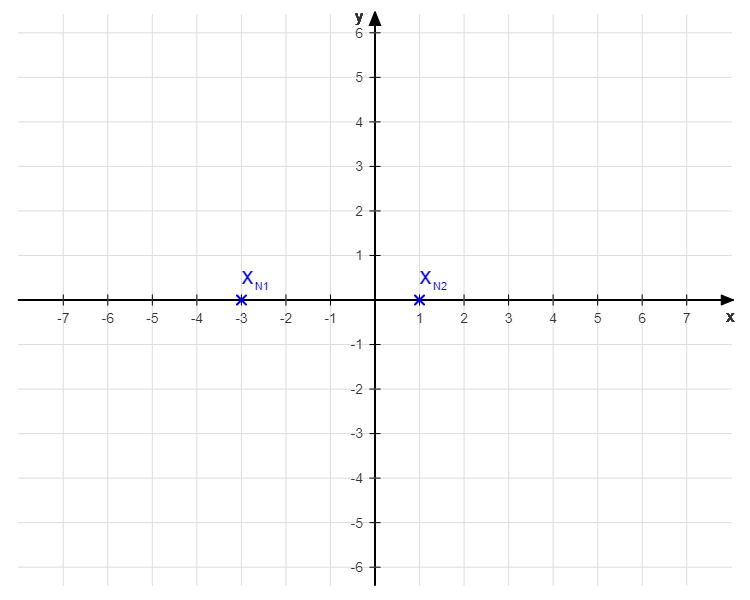
Nullstellen im Koordinatensystem:
Beispiel:
f(x) = x2 - 2·x - 3 | Null setzen
x2 - 2·x - 3 = 0 | Lösen mit pq-Formel
Lösungen (vgl. Rechner):
xN1 = -3
xN2 = 1
6. Schnittpunkt mit y-Achse
Den Schnittpunkt mit der y-Achse (auch „y-Achsenabschnitt“ genannt) ermitteln wir, indem wir bei der Funktionsgleichung x = 0 einsetzen.
Kurz: x = 0. Berechne f(0) = y.
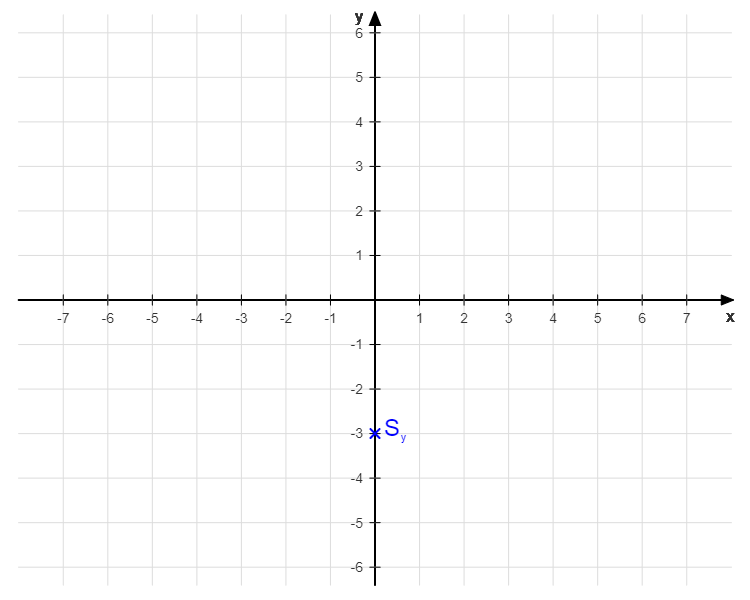
y-Achsenabschnitt im Koordinatensystem:
Beispiel:
f(x) = x2 - 2·x - 3 | x = 0
f(0) = 02 - 2·0 - 3
f(0) = -3
Lösung:
Sy(0|-3)
Bei Sy(0|-3) befindet sich also der Schnittpunkt des Graphen mit der y-Achse.
7. Extrempunkte
Extrempunkte können sein: Tiefpunkt oder Hochpunkt. Sie sind besonders auffällige Punkte des Graphen.
Um Extrempunkte zu bestimmen, müssen wir die erste Ableitung der Funktionsgleichung aufstellen und diese dann null setzen. So lässt sich die jeweilige Extremstelle berechnen.
Es handelt sich bei einem Punkt um einen Extrempunkt, wenn die erste Ableitung 0 ist und die zweite Ableitung ungleich 0. Kurz: \( f'(x_E) = 0 \) und \( f''(x_E) ≠ 0 \)
Hierbei gibt es Fallunterscheidungen, die wir mit der zweiten Ableitung vornehmen. Wir setzen die Extremstelle in die zweite Ableitung und wenn der Wert größer 0 ist, dann handelt es sich um einen Tiefpunkt. Ist der Wert kleiner 0, dann handelt es sich um einen Hochpunkt.
\( f''(x_E) \gt 0 \) → Tiefpunkt
\( f''(x_E) \lt 0 \) → Hochpunkt
Abschließend ist der ermittelte Wert xE in die Funktionsgleichung f(x) einzusetzen. Der berechnete y-Wert gibt dann die y-Koordinate des Extrempunktes an.
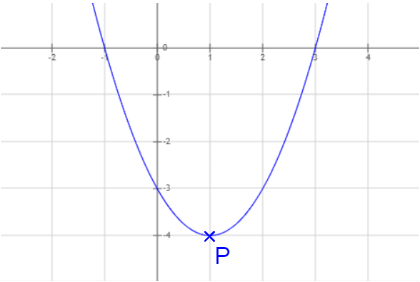
Extrempunkte des Graphen im Koordinatensystem:
Beispiel der Berechnung von Extremstellen:
Zuerst sind die Ableitungen zu bilden:
f(x) = x2 - 2·x - 3
f'(x) = 2·x - 2
f''(x) = 2
f'''(x) = 0
Dann können wir die erste Ableitung null setzen.
f'(x) = 2·x - 2
2·x - 2 = 0 | +2
2·x = 2 | :2
x = 1
Bei x = 1 haben wir also eine mögliche Extremstelle.
Ob es tatsächlich eine Extremstelle ist, muss nun noch mit der zweiten Ableitung überprüft werden:
f''(x) = 2 | x = 1
f''(1) = 2
Der in die zweite Ableitung eingesetzte x-Wert ergibt 2, damit handelt es sich um einen Tiefpunkt.
Bestimmen wir die y-Koordinate des Extrempunktes, indem wir x = 1 in die Funktionsgleichung einsetzen:
f(x) = x2 - 2·x - 3 | x = 1
f(1) = 12 - 2·1 - 3
f(1) = -4
Bei Sy(1|-4) befindet sich also der Extrempunkt des Graphen.
~plot~ x^2-2x-3;{1|-4};[[-3|5|-5|1]];noinput;nolabel ~plot~
Anhand des Graphen können wir sehen, dass es sich um einen Tiefpunkt handelt. Rechnerisch bestimmen wir dies mit der zweiten Ableitung, in die wir x = 1 einsetzen.
Hochpunkt oder Tiefpunkt:
f''(x) = 2 | x = 1
f''(1) = 2
2 ist größer als 0, daher Tiefpunkt.
8. Wendepunkte
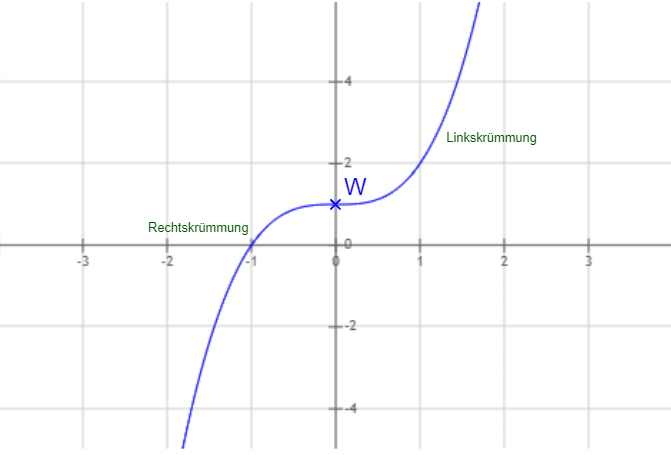
Wendepunkte sind Punkte des Graphen, bei denen sich das Krümmungsverhalten des Graphen ändert. Ab diesem Punkt wechselt der Graph von einer Rechtskurve zu einer Linkskurve oder von einer Linkskurve zu einer Rechtskurve.
Es handelt sich bei einem Punkt um einen Wendepunkt, wenn die zweite Ableitung 0 ist und die dritte Ableitung ungleich 0.
Kurz: \( f''(x_W) = 0 \) und \( f'''(x_W) ≠ 0 \)
Dann: Wendepunkt
Wendepunkt im Koordiantensystem. Beispiel:
Berechnung von Wendestellen anhand eines Beispiel:
Nehmen wir als Funktionsgleichung: f(x) = x3 + 1
Zuerst sind die Ableitungen zu bilden:
f(x) = x3 + 1
f'(x) = 3·x2
f''(x) = 6·x
f'''(x) = 6
Dann können wir die zweite Ableitung null setzen.
f''(x) = 6·x
6·x = 0 | :6
x = 0
Bei x = 0 haben wir also eine mögliche Wendestelle.
Nun müssen wir prüfen, ob die dritte Ableitung für diesen Wert ungleich 0 ist. Also f'''(x) ≠ 0:
f'''(x) = 6 | x = 0
f'''(6) = 6 → 6 ≠ 0 → Wendepunkt
Dies trifft zu, also ist es tatsächlich ein Wendepunkt.
Sollte der Wert gleich 0 sein, so kann keine direkte Aussage getroffen. (Üblicherweise behilft man sich dann mit dem Vorzeichenwechsel-Kriterium oder überprüft weitere Ableitungen, was aber in diesem Artikel zu weit führen würde.)
Bestimmen wir die y-Koordinate des Wendepunktes, indem wir x = 0 in die Funktionsgleichung einsetzen:
f(x) = x3 + 1 | x = 0
f(0) = 03 + 1
f(0) = 1
Bei W(0|1) befindet sich also der Wendepunkt des Graphen.
~plot~ x^3+1;{0|1};[[-5|5|-5|5]];noinput;nolabel ~plot~
Bei dem anderen Beispiel mit der Parabel gibt es übrigens keinen Wendepunkt. Die Parabel ist im Intervall ]-∞; ∞[ linksgekrümmt. Siehe Graph:
~plot~ x^2-2x-3;{1|-4};[[-3|5|-5|1]];noinput;nolabel ~plot~
Bei einem Wendepunkt hat die erste Ableitung meistens einen Wert größer oder kleiner 0 (d. h. in dem Punkt hat der Graph eine Steigung). Ergibt die erste Ableitung jedoch gleich 0 (es liegt keine Steigung vor), so handelt es sich um einen sogenannten Sattelpunkt.
Sattelpunkte erkennen wir also daran, dass: f'(x) = 0, f''(x) = 0 und f'''(x) ≠ 0.
Ein Sattelpunkt ist übrigens kein Extrempunkt, auch wenn die erste Ableitung hier ebenfalls 0 ist. Die zweite Ableitung ist beim Sattelpunkt hingegen 0, was bei Extrempunkten nicht erlaubt ist.
Der Graph der Funktion f(x) = x3 hat beispielsweise in P(0|0) einen Sattelpunkt.
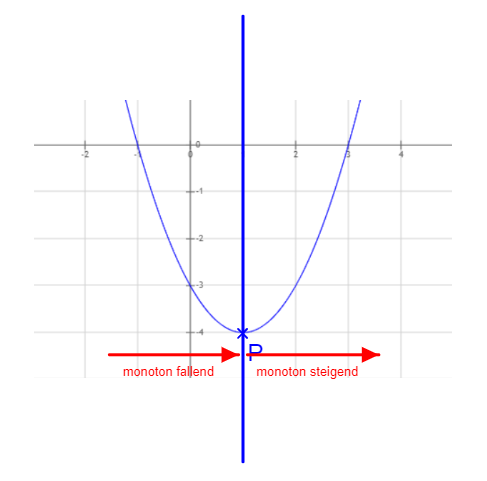
9. Monotonieverhalten
Das Monotonieverhalten gibt an, in welchen Intervallen der Funktionsgraph monoton steigend oder monoton fallend ist.
Hierbei hilft uns die erste Ableitung, denn sind deren Funktionswerte größer gleich 0 (also \( f'(x) \geq 0 \)), dann ist der Graph monoton steigend.
Sind die Funktionswerte der ersten Ableitung jedoch kleiner gleich 0 (also \( f'(x) \leq 0 \)), dann ist der Graph monoton fallend.
Die bestimmten Extrempunkte helfen uns zu erkennen, wo es einen Monotoniewechsel gibt.
Siehe hierzu auch noch mal: Grafisches Ableiten und Monotonie bei Funktionen.
Monotonieverhalten des Graphen im Koordinatensystem. Beispiel:
Die Monotonie wird mit Intervallen angegeben. Für das Beispiel oben:
]-∞; 1] monoton fallend
[1; +∞[ monoton steigend
10. Krümmungsverhalten
Das Krümmungsverhalten gibt an, in welchen Intervallen der Funktionsgraph rechtsgekrümmt oder linksgekrümmt ist.
Hierbei hilft uns die zweite Ableitung, denn sind deren Funktionswerte größer 0 (also \( f''(x) \gt 0 \)), dann ist der Graph linksgekrümmt.
Sind die Funktionswerte der zweiten Ableitung jedoch kleiner 0 (also \( f''(x) \lt 0 \)), dann ist der Graph rechtsgekrümmt.
Siehe hierzu auch noch mal: Grafisches Ableiten und Monotonie bei Funktionen.
Anhand des Wendepunktes können wir erkennen, wo es einen Krümmungswechsel gibt.
Krümmungsverhalten des Graphen im Koordinatensystem. Beispiel:
Die Krümmung wird mit Intervallen angegeben:
]-∞; 0[ rechtsgekrümmt
]0; +∞[ linksgekrümmt
11. Graph zeichnen
Auch wenn wir den Graphen schon mehrfach zuvor gesehen und als visuelle Hilfe genutzt haben, ist nun der eigentliche Zeitpunkt gekommen, den Graphen mit den gewonnenen Erkenntnissen zu zeichnen.
Der Graph der Funktion wird am Ende jeder Kurvendiskussion gezeichnet. Hierzu verwenden wir alle Punkte, die wir ermittelt haben. Auch das Monotonie und Krümmungsverhalten. Ggf. erstellen wir zusätzlich eine Wertetabelle, um weitere Punkte zum Zeichnen zu erhalten.
Wenn man einen grafischen Taschenrechner (GTR) besitzt, kann man diesen unter Umständen verwenden.
Oder man verwendet einen Funktionsplotter wie Plotlux.
Beispiel eines gezeichneten Graphen:
~plot~ x^2-2x-3;{1|-4};[[-3|5|-5|1]];noinput;nolabel ~plot~
Damit ist die Kurvendiskussion abgeschlossen.
Dieser Artikel hat die Kurvendiskussion allgemein behandelt. Als nächstes führen wir die Kurvendiskussion konkret durch: