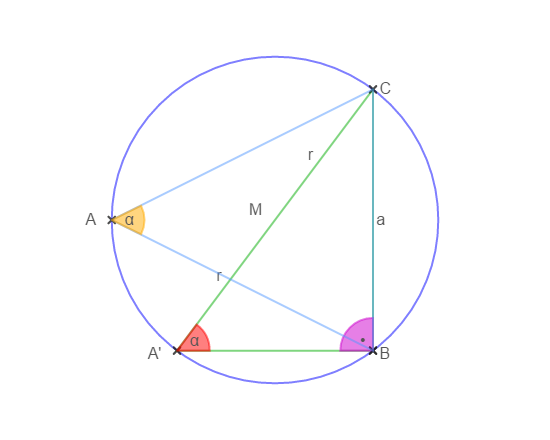
Gegeben sei das Dreieck ABC mit Umkreis, Radius r und Mittelpunkt M:
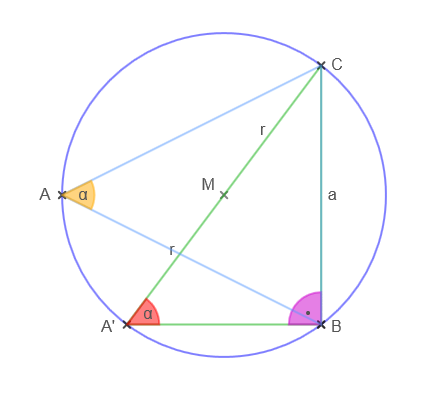
Die Dreiecksseite a ist eine Sehne des Umkreises, der Winkel α ist Umfangswinkel zur Sehne a. Alle Umfangswinkel zur Sehne a sind nach dem Umfangswinkelsatz gleich (auf der selben Seite des Kreises), also auch der rechte Winkel bei Punkt B.
In diesem Fall verläuft die Strecke A'C durch den Mittelpunkt M des Umkreises (Satz des Thales) und es ist Strecke |A'C| = 2·r.
Im rechtwinkligen Dreieck A'BC gilt dann: \( \sin(α) = \frac{a}{2·r} \) und das können wir umstellen zu: \( \frac{a}{ \sin(α) } = 2 · r \)