Lösen von Sinusgleichungen der Form sin(b·x + c) + d = 0

Betrachten wir uns die Nullstellen und halten fest, dass wir die Nullstellen nicht verändern, wenn wir den Graphen strecken oder stauchen:

~plot~ sin(x);2*sin(x);5*sin(x);hide ~plot~

Addieren wir jedoch einen Wert d herauf, so ändern sich alle Nullstellen:

~plot~ sin(x)+0.5;2*sin(x)+0.5;5*sin(x)+0.5;0.5;hide ~plot~

Jede Nullstelle bzw. jeder Punkt der Nullstellen verschiebt sich um 0,5 nach oben.

Lösungsformel für Nullstellen von sin(b·x + c) + d = 0

Unter Berücksichtigung von d lässt sich folgende allgemeine Lösungsformel für Nullstellen herleiten:

sin(b·x + c) + d = 0 | -d
sin(b·x + c) = -d | sin^-1
b·x + c = sin^-1(-d)
b·x + c = sin^-1(-d) | -c
b·x = sin^-1(-d) - c | :b
x = (sin^-1(-d) - c) / b

Berechnen wir noch eine Beispielaufgabe, um sicherer zu werden:

sin(2·x+30°) - 0,5 = 0

Lösungsformel:
x = (sin^-1(-d) - c) / b

x = (sin^-1(-(-0,5)) - 30°) / 2
x = (sin^-1(0,5) - 30°) / 2
x = (30° - 30°) / 2
x = 0° / 2
x = 0°

Überprüfen wir die Lösung x = 0° graphisch:

~plot~ sin(2x+30/180*pi)-0,5;x=0;hide ~plot~

Wir sehen die Nullstelle bei 0°.

Wenn wir die Lösungen im Falle eines unbeschränkten Intervalls benötigen, so müssen wir noch die Periode bestimmen.

Periode T = 360°/ b
Periode T = 360°/ 2 = 180°

Periode in Bogenmaß T = 180°/180° · π = 1· π ≈ 3,1416

Die Nullstellenformel lautet damit:

x₁ = 0° + k·180°

Zeichnen wir den Graphen und schauen, ob wir die Nullstelle wiederfinden:

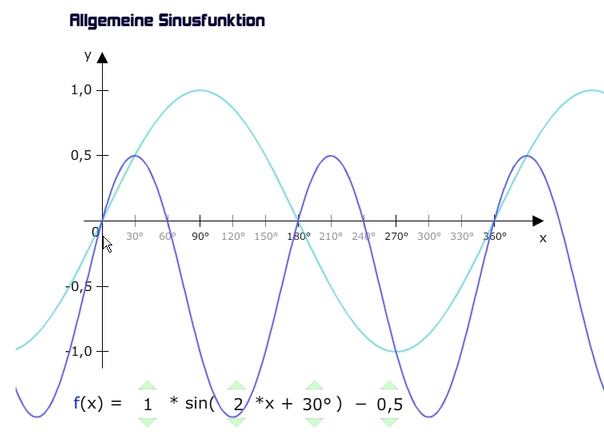
Die erste Nullstelle ist bei x = 0°, eine weitere bei 180°. Doch es gibt noch eine zweite Nullstelle bei 60°, wie rechnen wir diese aus? Hierzu nutzen wir erneut die Identitäten:

sin(x) = sin(180° - x)

Jedoch ist unser Term nicht x, sondern vielmehr 2x+30°. Dieses müssen wir nun für die Identitätsformel einsetzen:

sin(2x+30°) = sin(180° - (2x+30°))

Formen wir das um:

sin(2x+30°) = sin(180° - 2x - 30°)
sin(2x+30°) = sin(150° - 2x)

Und setzen wir nun die Nullstelle x₁ = 0 ein.

sin(2x+30°) = sin(150° - 2x) | x = 0
sin(2·0+30°) = sin(150° - 2·0)
sin(30°) = sin(150°)

Nun müssen wir den x-Wert bestimmen, der zu 150° führt.

sin(2x+30°) = sin(150°)
2x+30° = 150°    | -30°
2·x = 120°       | :2
x = 60°

Die zweite Nullstelle liegt also bei 60°. Auch hier legen wir den Periodensummanden fest:

Periode T = ^360°/_b
Periode T = ^360°/₂ = 180°

x₂ = 60° + k·180°

Die Lösungen für die Nullstellen zusammengefasst:

x₁ = 0° + k·180°

x₂ = 60° + k·180°

Tipp: Das Programm Nullstellen bei Sinusfunktionen bestimmen hilft, ermittelte Lösungen bei verschiedenen Aufgaben auf Richtigkeit zu überprüfen.