Die allgemeine Tangensgleichung lautet:
a·tan(b·x + c) + d = 0
Wir wollen die Nullstellen ermitteln, tun wir das an einem Beispiel:
f(x) = 0,3·tan(1,5·x - 90°) + 0,3
Zuerst schauen wir uns den Graphen an:
~plot~ 0.3*tan(1.5*x-90/180*pi)+0*3;zoom[[4]];hide ~plot~
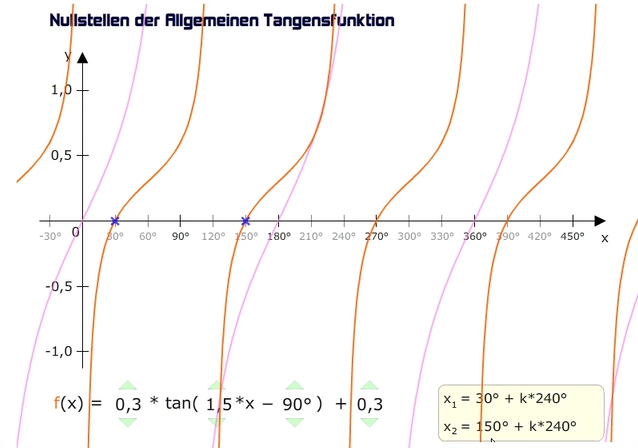
Wir erkennen die ersten beiden Nullstellen bei 30° und 150°. Berechnen wir diese statt sie nur abzulesen:
0,3·tan(1,5·x - 90°) + 0,3 = 0 | -0,3
0,3·tan(1,5·x - 90°) = -0,3 | :0,3
tan(1,5·x - 90°) = -1 | tan-1
1,5·x - 90° = tan-1(-1)
1,5·x - 90° = -45° | +90°
1,5·x = 45° | :1,5
x1 = 30°
Die Periode bei tan(x) geht von 0° bis 180°. Bei dem Beispiel haben wir jedoch b = 1,5, damit ergibt sich eine Periode von T = 180° / 1,5 = 120°.
Nun können wir rechnen:
x2 = x1 + T | x1 = 30°, T = 120°
x2 = 30° + 120°
x2 = 150°
Ohne Einschränkung des Intervalls müssen wir noch den Periodizitätssummanden einbringen:
x1 = 30° + k·120°
x2 = 150° + k·120°
Wir können beide Ergebnisse zusammenfassen, denn x₂ ergibt sich aus der Formel mit x₁, wenn wir k = 1 einsetzen (x₁ = 30° + 1·120° = 150°). Wir laufen alle Nullstellen mit der +k·120° ab, die Lösung für alle Nullstellen lautet also:
x = 30° + k·120°
Es gibt auch Gleichungen, die weitaus schwieriger sind, wie zum Beispiel sin(x)·cos(20°)+cos(x)·sin(20°) = 1. Für Lösungen solcher Gleichungen benötigen wir die sogenannten Additionstheoreme.

