Lektion DIF03: Differentialrechnung
Differentialrechnung - Voraussetzungen zum Verstehen
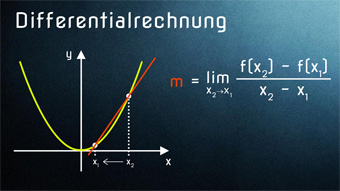
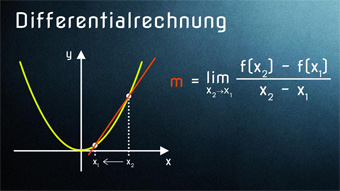
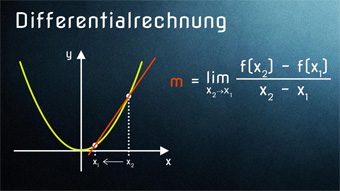
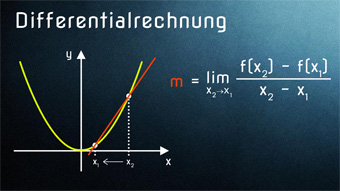
Nötige Voraussetzungen zum Einstieg in die Differentialrechnung: Lineare Funktionen, Grenzwert (Limes), grafisches Ableiten. Wir lernen den Differenzenquotienten kennen.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
DIF03-2 Differentialrechnung - Funktion rechnerisch ableitenWas ist die Differentialrechnung. Vom Differenzenquotient zum Differentialquotient. Wie wird mit Differentialquotient die rechnerische Ableitung gebildet. Hilfsmittel Limes.
-
DIF03-3 Differentialrechnung - h-MethodeMit Hilfe einer Ableitungsfunktion kann man die Steigung an einer Stelle sofort berechnen. Mit der h-Methode können wir diese Funktionsgleichung ermitteln.
-
DIF03-4 Differentialrechnung - AbleitungsregelnWir lernen die wichtigen Ableitungsregeln kennen: Potenzregel mit f(x)=x^n zu f`(x)=n·x^(n-1) sowie Faktorregel und konstante Funktion. Hinweise zur E-Funktion und deren Ableitung. Ableitung von Sinus und Kosinus.
-
DIF03-5 Differentialrechnung - AbleitungsregelnWir lernen die Ableitungsregeln kennen: Potenzregel, konstante Funktion, Faktorregel, Summenregel, Produktregel, Quotientenregel, Kettenregel. Inkl. Beispielrechnungen.
Hier findet ihr ein Programm für die Ableitung von Polynomfunktionen, einfach Funktionsgleichung eingeben und der Graph sowie der Graph der Ableitungsfunktion werden euch angezeigt: Programm zu Ableitungen für Funktionen von x bis x13
Die in den Videos eingesetzten Programme findet ihr bei Desmos.com:
- Graph einer quadratischen Funktion und Graph der Ableitungsfunktion
- Sekante am Graph der quadratischen Funktion f(x)=x²
- Sekante am Graph der quadratischen Funktion f(x)=-x²+5
- Graph der konstanten Funktion f(x)=3 und deren Ableitungsfunktion f′(x)=0
- Graph der kubischen Funktion f(x)=x³-4x und deren Ableitungsfunktion
- Graph der Sinusfunktion und deren Ableitung
- Graph der Kosinusfunktion und deren Ableitung
Hierzu gibt es keine Lernprogramme.
Hier findest du 8 Arbeitsblätter, mit denen du dein Wissen testen kannst.
-
AB: Lektion Differentialrechnung (Teil 1)
-
AB: Lektion Differentialrechnung (Teil 2)
-
AB: Lektion Differentialrechnung (Teil 3)
-
AB: Lektion Differentialrechnung (Teil 4)
-
AB: Lektion Differentialrechnung (Teil 5)
-
AB: Lektion Differentialrechnung (Teil 6)
-
AB: Lektion Differentialrechnung (Teil 7)
-
AB: Lektion Differentialrechnung (Teil 8)
Hier findest du 2 Lernchecks, mit denen du dein Wissen testen kannst.
Artikel im Wiki:
- Grafisches Ableiten
- Graphen und ihre Ableitungen (Beispiele)
- Differentialrechnung - Einführung
- Differenzenquotient
- Differentialquotient
- h-Methode (mit Beispiel)
- Ableitung (mit Beispiel)
- Ableitungsregeln Übersicht
- Potenzregel (Ableitung)
- Faktorregel (Ableitung)
- Summenregel (Ableitung)
- Produktregel (Ableitung)
- Quotientenregel (Ableitung)
- Kettenregel (Ableitung)
- Übersicht 1. und 2. Ableitungen von Funktionen
- Zusammenfassung zur Differentialrechnung
- Vorgehen bei Extremwertaufgaben
Häufige Fragen:
- Ableitungen von 2 Funktionen: f(x)=ax² und g(x)=1/(2x²)
- Produktregel für f(x) = x*Wurzel x?
- Wie lautet die Ableitung von 1/(3-x)?
- An welcher Stelle hat f(x)=x^3+2 die Steigung 4?
- Ableitung der Funktion f(x) = x²+3 (h-Schreibweise)
- Ableitung der Funktion f(x)=-x^{-2} (h-Schreibweise)
- Erste Ableitung von f(x)=(x²-4)/(x²+8)
- Weshalb ist die Ableitung von Sinus gleich Kosinus?
Finde weitere Fragen und Antworten in der Mathelounge.