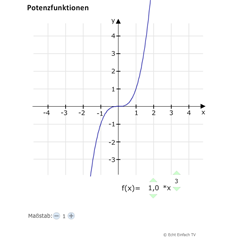
Lektion F12: Potenzfunktionen
Potenzfunktionen: Symmetrie, Monotonie, Definitions-/Wertebereich
Was ist eine Potenzfunktion? Aufbau f(x) = a·x^n. Symmetrie bei geraden und ungeraden Exponenten (Achsensymmetrie und Punktsymmetrie). Gerade und ungerade Funktionen. Monotonieverhalten. Definitionsmenge und Wertebereich.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
F12-2 Potenzfunktionen: Gemeinsame Punkte, HyperbelGemeinsame Punkte bei Potenzfunktionen je nach geradem/ungeradem Exponent. Es entsteht eine Hyperbel, wenn der Exponent negativ wird, Beispiel: f(x)=x^(-1). Wie kommt es bei negativen Exponenten zur Definitionslücke bei x=0.
-
F12-3 Potenzfunktionen mit negativen ExponentenEigenschaften von Potenzfunktionen mit negativen Exponenten: Symmetrieverhalten, Monotonieverhalten, Definitionsmenge/Wertebereich, gemeinsame Punkte. Definitionslücken.
-
F12-4 Gleichung der Potenzfunktion aus 2 Punkten bestimmenWir bestimmen aus 2 gegebenen Punkten die Funktionsgleichung einer Potenzfunktion. Lösen per Logarithmus. Lösen mit Hilfe eines linearen Gleichungssystems.
-
F12-5 Schnittpunkte von 2 PotenzfunktionenWir berechnen die Schnittpunkte von 2 Potenzfunktionen mittels Gleichsetzen. x-Wert zu gegebenem Funktionswert bei einer Potenzfunktion ermitteln. Auswirkungen des Vorfaktors a bei f(x)=a·x^n auf den Graphen der Funktion.
Nutzt alternativ dieses Programm: Potenzfunktionen (Desmos)
Hier findest du 3 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 1 Lerncheck, mit dem du dein Wissen testen kannst.
Häufige Fragen:
Finde weitere Fragen und Antworten in der Mathelounge.