Lektion G25: Bruchgleichungen / Bruchterme
In dieser Lektion lernen wir, mit welchen Werkzeugen wir Bruchgleichungen lösen können: Erweitern von Brüchen, um gleichnamige Nenner zu bilden, Gleichungen umstellen, Binomische Formel und p-q-Formel.
Nachdem ihr die Videos gesehen habt, werdet ihr in der Lage sein, alle möglichen Bruchgleichungen selbstständig zu lösen.
Zu Beginn des ersten Videos wiederholen wir einige wesentliche Inhalte.
Es wäre trotzdem sinnvoll, wenn ihr die Lektionen Brüche und Terme und Gleichungen vorher gesehen habt. Dann kann es losgehen.
Bruchgleichungen - Einführung und Voraussetzungen
Was ist eine Bruchgleichung. Wiederholung des Wissens zu den Brüchen und zum Umformen von Gleichungen. Lösen der Bruchgleichung 2/x = 0,5 durch Umformen der Gleichung. Lösen von 2/(x+3) = 5 mit Probe.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
G25-2 Bruchgleichungen - Lösung durch Umformen und ErweiternLösung durch Umformen von Gleichungen und Erweitern der Brüche (Nenner gleichnamig machen): Wir berechnen 1/(x+8) = 5/x und 2/x + 1/2x = 5. Auch machen wir jeweils die Probe. Zusätzlich lösen wir den Term 10x²+5x=0. Einführung und Bedeutung der Definitionsmenge.
-
G25-3 Bruchgleichungen - Lösen mit Hilfe der Binomischen FormelDefinitionsmenge bestimmen bei 2/(x+2) und 5/(x-2). Lösen der Bruchgleichung 2/(x+2) + 5/(x-2) = 20/(x²-4) mit Hilfe der Binomischen Formel (gleichnamige Nenner). Leere Lösungsmenge. Lösen der Bruchgleichung 2/(x+2) + 1/(x-2) = 1/(x²-4). Probe.
-
G25-4 Bruchgleichungen - Lösen mit Ausklammern und ErweiternLösen der Gleichung (x-1)/(4x+2) + 9/4 = 3/(2x+1) durch Bilden eines gemeinsamen Nenners mittels Ausklammern und Erweitern. Lösen von 3/a - 2/3a + 1/6a = 5 sowie 3/(n-1) = 4/(n-2). Bestimmen der Definitionsmenge und Überprüfen des Ergebnisses.
-
G25-5 Bruchgleichungen - Lösen mit Normalform und p-q-FormelLösen von (x+1)/x + (x+2)/x = x mittels Umformung in die Normalform und Anwenden der p-q-Formel. Zusammenfassung des Wissens. Abschließende Übungsaufgaben mit Lösung: (1+b)/2b = 5/4b + 1/4 und 5/2y + 4/3y = 7/2 und 3/(z-3) - 2/(z-3) = 4/(z²-6z+9)
Im Folgenden findet ihr einige Programme zu den Brüchen, mit denen ihr euer Wissen auffrischen könnt:
-
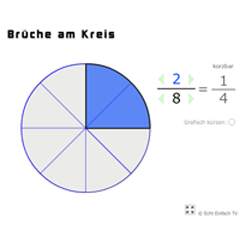 Brüche am KreisStellt Zähler und Nenner des Bruches ein und erkennt die Anteile am Kreis. Falls der Bruch kürzbar ist, wird dies angezeigt.
Brüche am KreisStellt Zähler und Nenner des Bruches ein und erkennt die Anteile am Kreis. Falls der Bruch kürzbar ist, wird dies angezeigt. -
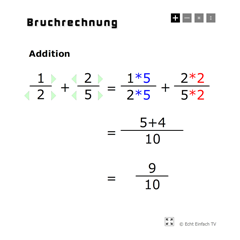 Bruchrechnung (Grundrechenarten)Die vier Grundrechenarten bei beliebigen Brüchen mit Rechenweg, inklusive Erweitern und Kürzen.
Bruchrechnung (Grundrechenarten)Die vier Grundrechenarten bei beliebigen Brüchen mit Rechenweg, inklusive Erweitern und Kürzen. -
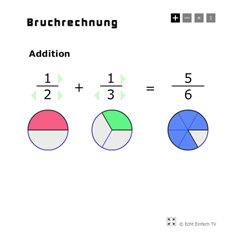 Bruchrechnung (als Flächen)Mit diesem Programm könnt ihr beliebige Brüche berechnen, die gleichzeitig als Flächen angezeigt werden.
Bruchrechnung (als Flächen)Mit diesem Programm könnt ihr beliebige Brüche berechnen, die gleichzeitig als Flächen angezeigt werden. -
 Spiel: Brüche QuizZeigt in diesem Brüche-Spiel, dass ihr die Bruchrechnung beherrscht. In nur 3 Minuten müsst ihr so viele Aufgaben wie möglich richtig berechnen!
Spiel: Brüche QuizZeigt in diesem Brüche-Spiel, dass ihr die Bruchrechnung beherrscht. In nur 3 Minuten müsst ihr so viele Aufgaben wie möglich richtig berechnen!
Hier findest du 4 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 5 Lernchecks, mit denen du dein Wissen testen kannst.
Häufige Fragen:
Finde weitere Fragen und Antworten in der Mathelounge.