Approximation von Funktionen
Irrationale Funktionen können in Potenzreihen entwickelt werden. Dieser Ansatz kann auch zur Approximation von Messwerten angewendet werden, um so einen funktionellen Zusammenhang zwischen den Werten herstellen zu können. Damit kann erreicht werden, dass das Verhalten des Messobjektes an Stellen, die noch nicht vermessen wurden, in bestimmten Grenzen vorhergesagt werden kann. Mit dem Ansatz
\(f(x) = {a_0} + {a_1}x + {a_2}{x^2} + {a_3}{x^3} + ..... \) Gl. 111
und einem gegebenen Set von Paaren von Messwerten (xn;y n) wird die Approximation in ein Polynom N-ten Grades vorgenommen. Dazu sind die Koeffizienten in Gl. 111 zu bestimmen. Es ist leicht zu sehen, dass diese Aufgabe in die Lösung eines linearen Gleichungssystems bestehend aus N Gleichungen mit N Unbekannten – nämlich den N Koeffizienten – überführt werden kann. Dazu werden alle N Paare von Messwerten nacheinander in Gl. 111 eingesetzt:
\( \begin{array}{l}{y_1} = {a_0} + {a_1}{x_1} + {a_2}{x_1}^2 + {a_3}{x_1}^3 + ..... + {a_N}{x_1}^N\\{y_2} = {a_0} + {a_1}{x_2} + {a_2}{x_2}^2 + {a_3}{x_2}^3 + ..... + {a_N}{x_2}^N\\{y_3} = {a_0} + {a_1}{x_3} + {a_2}{x_3}^2 + {a_3}{x_3}^3 + ..... + {a_N}{x_3}^N\\\\{y_n} = {a_0} + {a_1}{x_n} + {a_2}{x_n}^2 + {a_3}{x_n}^3 + ..... + {a_N}{x_n}^N & u.s.w. & \end{array} \) Gl. 112
Beachte: nicht die xn sind die unbekannten Größen, sondern die Koeffizienten an!
In Determinantenschreibweise lautet die Lösung z.B. für den Koeffizienten a0:
\( D = \left|{ \begin{array}{cc} 1&{ {x_1} }&{x_1^2}&{...}&{x_1^N}\\1&{ {x_2} }&{x_2^2}&{...}&{x_2^N}\\1&{ {x_3} }&{x_3^2}&{...}&{x_3^N}\\{...}&{...}&{...}&{x_{_n}^n}&{...}\\1&{ {x_N} }&{x_N^2}&{...}&{x_{_N}^N}\end{array} }\right| \qquad {D_{ {a_0} } } = \left|{ \begin{array}{cc}{ {y_1} }&{ {x_1} }&{x_1^2}&{...}&{x_1^N}\\{ {y_2} }&{ {x_2} }&{x_2^2}&{...}&{x_2^N}\\{ {y_3} }&{ {x_3} }&{x_3^2}&{...}&{x_3^N}\\{...}&{...}&{...}&{x_{_n}^n}&{...}\\{ {y_N} }&{ {x_N} }&{x_N^2}&{...}&{x_{_N}^N}\end{array} }\right| \) Gl. 113
nach der Cramerschen Regel ergibt sich der Wert für den Koeffizienten a0 zu:
\({a_0} = \frac{ { {D_{ {a_0} } } } }{D}\) Gl. 114
analog ergeben sich dann auch die weiteren Koeffizienten nach den Regeln der Determinantenrechnung.
Beispiel:
Gegeben sind die vier Werte-Paare (-2;1), (-1;0), (1;0) und (2;-2) einer Messreihe. Welcher Wert ist an der Stelle x = 0,5 zu erwarten?
Lösung:
\(D = \left| {\begin{array}{cc}1&{ - 2}&4&{ - 8}\\1&{ - 1}&1&{ - 1}\\1&1&1&1\\1&2&4&8\end{array} } \right|\,\,\,\,\,\,\,\) \({D_{ {a_0} } } = \left| {\begin{array}{cc}1&{ - 2}&4&{ - 8}\\0&{ - 1}&1&{ - 1}\\0&1&1&1\\{ - 2}&2&4&8\end{array} } \right|\,\,\,\,\,\,\,\,\,{D_{ {a_1} } } = \left| {\begin{array}{cc}1&1&4&{ - 8}\\1&0&1&{ - 1}\\1&0&1&1\\1&{ - 2}&4&8\end{array} } \right|\,\,\,\,\,\,\,\,\,\,{D_{ {a_2} } } = \left| {\begin{array}{cc}1&{ - 2}&1&{ - 8}\\1&{ - 1}&0&{ - 1}\\1&1&0&1\\1&2&{ - 2}&8\end{array} } \right|\,\,\,\,\,\,\,\,{D_{ {a_3} } } = \left| {\begin{array}{cc}1&{ - 2}&4&1\\1&{ - 1}&1&0\\1&1&1&0\\1&2&4&{ - 2}\end{array} } \right|\,\)
und \({a_0} = \frac{ { {D_{ {a_0} } } } }{D};\,\,\,\,\,{a_1} = \frac{ { {D_{ {a_1} } } } }{D};\,\,\,\,{a_2} = \frac{ { {D_{ {a_2} } } } }{D};\,\,\,\,{a_3} = \frac{ { {D_{ {a_3} } } } }{D}\)
Bestimmung der Koeffizienten-Determinante:
1. Vereinfachung durch Erzeugen von Nullen in der ersten Spalte der 2. bis 4. Zeile.
\(D = \left| {\begin{array}{cc}1&{ - 2}&4&{ - 8}\\1&{ - 1}&1&{ - 1}\\1&1&1&1\\1&2&4&8\end{array} } \right|\, = \,\left| {\begin{array}{cc}1&{ - 2}&4&{ - 8}\\0&1&{ - 3}&7\\0&3&{ - 3}&9\\0&4&0&{16}\end{array} } \right|\, = 1 \cdot \left| {\begin{array}{cc}1&{ - 3}&7\\3&{ - 3}&9\\4&0&{16}\end{array} } \right|\, = - 48 - 108 + 84 + 144 = 72\,\,\,\)
analog dazu erfolgt die Berechnung der Zählerdeterminanten:
\( {D_{ {a_0} } } = \left|{ \begin{array}{cc} 1 & {-2} & 4 & {-8} \\ 0 & { - 1} & 1 & {-1} \\ 0 & 1 & 1 & 1 \\ {-2} & 2 & 4 & 8 \end{array} } \right| \, = \, \left|{ \begin{array}{cc} 1 & {-2} & 4 & {-8} \\ 0 & { - 1} & 1 & {-1} \\ 0 & 1 & 1 & 1 \\ 0 & { - 2} & {12} & {-8} \end{array} } \right| = 1 \cdot \left|{ \begin{array}{cc}{ - 1} & 1 & {-1} \\ 1 & 1 & 1\\{ - 2} & {12} & {- 8} \end{array} } \right| \, = 8 - 2 - 12 - 2 + 12 + 8 = 12 \Rightarrow {a_0} = \frac{1}{6} \)
\( {D_{ {a_1} } } = \left| {\begin{array}{cc}1&1&4&{ - 8}\\1&0&1&{ - 1}\\1&0&1&1\\1&{ - 2}&4&8\end{array} } \right| = \left| {\begin{array}{cc}1&1&4&{ - 8}\\1&0&1&{ - 1}\\1&0&1&1\\3&0&{12}&{ - 8}\end{array} } \right| = \left( { - 1} \right) \cdot \left| {\begin{array}{cc}1&1&{ - 1}\\1&1&1\\3&{12}&{ - 8}\end{array} } \right| = - \left( { - 8 + 3 - 12 + 3 - 12 + 8} \right) = 18 \Rightarrow {a_1} = \frac{1}{4} \)
\( {D_{ {a_2} } } = \left| {\begin{array}{cc}1&{ - 2}&1&{ - 8}\\1&{ - 1}&0&{ - 1}\\1&1&0&1\\1&2&{ - 2}&8\end{array} } \right| = \left| {\begin{array}{cc}1&{ - 2}&1&{ - 8}\\1&{ - 1}&0&{ - 1}\\1&1&0&1\\3&{ - 2}&0&{ - 8}\end{array} } \right|\, = 1 \cdot \left| {\begin{array}{cc}1&{ - 1}&{ - 1}\\1&1&1\\3&{ - 2}&{ - 8}\end{array} } \right|\, = - 8 - 3 + 2 + 3 + 2 - 8 = - 12 \Rightarrow {a_2} = - \frac{1}{6} \)
\( {D_{ {a_3} } } = \left| {\begin{array}{cc}1&{ - 2}&4&1\\1&{ - 1}&1&0\\1&1&1&0\\1&2&4&{ - 2}\end{array} } \right| = \left| {\begin{array}{cc}1&{ - 2}&4&1\\1&{ - 1}&1&0\\1&1&1&0\\3&{ - 2}&{12}&0\end{array} } \right| = \left( { - 1} \right) \cdot \left| {\begin{array}{cc}1&{ - 1}&1\\1&1&1\\3&{ - 2}&{12}\end{array} } \right| = - \left( {12 - 3 - 2 - 3 + 2 + 12} \right) = - 18 \Rightarrow {a_3} = - \frac{1}{4} \)
Damit lautet die approximierende Funktion:
\(y = \frac{1}{6} + \frac{1}{4}x - \frac{1}{6}{x^2} - \frac{1}{4}{x^3} \)
und die gesuchte Lösung lautet:
\( y(0,5)=0,219 \)
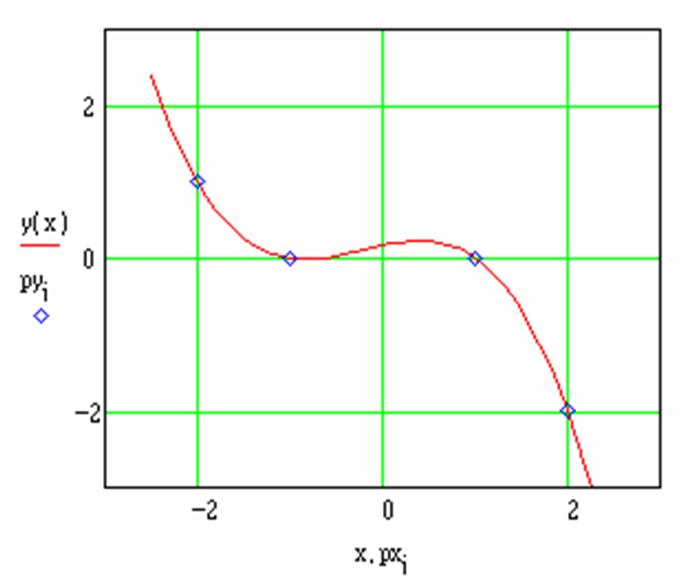
Bei der Auswahl der Wertepaare ist darauf zu achten, dass nur linear unabhängige Paare verwendet werden. Andernfalls führt das zu überbestimmten Gleichungssystemen.
Beispiel 2:
Gegeben sind die drei Werte-Paare (-2;1), (-1;0) und (1;-2) einer Messreihe gegeben. Welche Funktion approximiert diese Werte?
Lösung:
\(\begin{array}{l}D = \left| {\begin{array}{cc}1&{ - 2}&4\\1&{ - 1}&1\\1&1&1\end{array} } \right|\, = - 1 - 2 + 4 + 4 - 1 + 2 = 6\\\,\,\,\,\,\,\end{array}\)
\(\begin{array}{l}{a_0} = \frac{1}{6}\left| {\begin{array}{cc}1&{ - 2}&4\\0&{ - 1}&1\\{ - 2}&1&1\end{array} } \right|\, = \frac{1}{6}\left| {\begin{array}{cc}1&{ - 2}&4\\0&{ - 1}&1\\0&{ - 3}&9\end{array} } \right| = \frac{1}{6} \cdot 1 \cdot \left| {\begin{array}{cc}{ - 1}&1\\{ - 3}&9\end{array} } \right| = - 1\\\,\,\,\,\,\,\end{array}\)
\(\begin{array}{l}{a_1} = \frac{1}{6}\left| {\begin{array}{cc}1&1&4\\1&0&1\\1&{ - 2}&1\end{array} } \right|\, = \frac{1}{6}\left| {\begin{array}{cc}1&1&4\\1&0&1\\3&0&9\end{array} } \right| = \frac{1}{6} \cdot \left( { - 1} \right) \cdot \left| {\begin{array}{cc}1&1\\3&9\end{array} } \right| = - 1\\\,\,\,\,\,\,\end{array}\)
\(\begin{array}{l}{a_2} = \frac{1}{6}\left| {\begin{array}{cc}1&{ - 2}&1\\1&{ - 1}&0\\1&1&{ - 2}\end{array} } \right|\, = \frac{1}{6}\left| {\begin{array}{cc}1&1&1\\1&{ - 1}&0\\3&{ - 3}&0\end{array} } \right| = \frac{1}{6} \cdot 1 \cdot \left| {\begin{array}{cc}1&{ - 1}\\3&{ - 3}\end{array} } \right| = 0 \\ \end{array}\)
Damit lautet die approximierende Funktion: \(y = - 1 - x\)
Für die angegebenen Punkte ergibt sich eine lineare Funktion, einer der drei Messwerte ist überbestimmt!
Für den praktischen Gebrauch ist dieses Verfahren aber wenig geeignet. Einerseits ist der Berechnungsaufwand für die Koeffizienten des approximierenden Polynoms verhältnismäßig hoch, andererseits können weitere Wunscheigenschaften, wie etwa Flachheit (flatness) oder Steigungsanforderungen in bestimmten Stützpunkten nicht erfüllt werde. Andere Approximationen wie z.B. die SPLINE-Approximation sind daher wesentlich besser für diese Aufgabe geeignet.
Berechnung der Fläche beliebiger Dreiecke
Die gesuchte Fläche des grünen Dreiecks ergibt sich nach Abbildung 17 aus der Fläche des gelben Dreiecks (0;0 x2;0 x2;y2) abzüglich der Dreiecksfläche (0;0 x1;0 x1;y1) sowie der Trapezfläche ( x1;0 x2;0 x2;y2 x1;y1 ) .
\( F = \frac{1}{2}{x_2}{y_2} - \frac{1}{2}{x_1}{y_1} - \left( { {x_2} - {x_1} } \right)\frac{1}{2}\left( { {y_1} + {y_2} } \right) \) Gl. 115
\( \begin{array}{l}\,\,\,\,\, = \frac{1}{2}\left[ { {x_2}{y_2} - {x_1}{y_1} - {x_2}{y_1} + {x_1}{y_1} - {x_2}{y_2} + {x_1}{y_2} } \right]\\\,\,\,\,\, = \frac{1}{2}\left[ { {x_1}{y_2} - {x_2}{y_1} } \right]\end{array} \)

Der in eckigen Klammern stehende Ausdruck kann auch als eine Determinante ausgedrückt werden:
\(F = \frac{1}{2}\left| {\begin{array}{cc}{ {x_1} }&{ {y_1} }\\{ {x_2} }&{ {y_2} }\end{array} } \right|\) Gl. 116
Liegt nun das Dreieck, dessen Fläche gesucht ist, nicht im Koordinatenursprung (Abbildung 18), muss eine Koordinatentransformation vorgenommen werden, um das Ergebnis von Gl. 116 weiter verwenden zu können.

Mit der Transformation
\(\begin{array}{l}{x_1} \to {x_1} - {x_3}\\{x_2} \to {x_2} - {x_3}\\{y_1} \to {y_1} - {y_3}\\{y_2} \to {y_2} - {y_3}\end{array}\) Gl. 117
wird Gl. 116 in
\(F = \frac{1}{2}\left| {\begin{array}{cc}{\left( { {x_1} - {x_3} } \right)}&{\left( { {y_1} - {y_3} } \right)}\\{\left( { {x_2} - {x_3} } \right)}&{\left( { {y_2} - {y_3} } \right)}\end{array} } \right|\) Gl. 118
überführt.
Nach Abschnitt Eigenschaften drei- und mehrreihiger Determinanten wird die Determinante nach Gl. 118 durch Rändern erweitert:
\(F = \frac{1}{2}\left| {\begin{array}{cc}{\left( { {x_1} - {x_3} } \right)}&{\left( { {y_1} - {y_3} } \right)}&0\\{\left( { {x_2} - {x_3} } \right)}&{\left( { {y_2} - {y_3} } \right)}&0\\a&b&1\end{array} } \right|\) Gl. 119
Das hinzugefügte Element a33=1 verursacht, dass das Vorzeichen positiv ist.
Da die Größen a und b frei gewählt werden dürfen, werden a = x3 und b = y3 gewählt:
\(F = \frac{1}{2}\left| {\begin{array}{cc}{\left( { {x_1} - {x_3} } \right)}&{\left( { {y_1} - {y_3} } \right)}&0\\{\left( { {x_2} - {x_3} } \right)}&{\left( { {y_2} - {y_3} } \right)}&0\\{ {x_3} }&{ {y_3} }&1\end{array} } \right|\) Gl. 120
Eigenschaft h bei Eigenschaften zweireihiger Determinaten besagt, dass sich der Wert einer Determinante nicht ändert, wenn Vielfache einer Zeile zu anderen Zeilen addiert wird. Daher kann die dritte Zeile zu der ersten bzw. zweiten Zeile hinzu addiert werden:
\(F = \frac{1}{2}\left| {\begin{array}{cc}{ {x_1} }&{ {y_1} }&1\\{ {x_2} }&{ {y_2} }&1\\{ {x_3} }&{ {y_3} }&1\end{array} } \right|\) Gl. 121
Damit ist eine handliche Berechnungsvorschrift für beliebige Dreiecke an beliebigen Positionen im Koordinatensystem gegeben.
