In Anlehnung an die Lösungsgleichungen für sich schneidende Geraden werden Gleichungssysteme durch Umformung gelöst.
Zur Erinnerung sei die Gl. 61 nochmals notiert: \( \begin{array}{l} I. & {a_{11} }·x + {a_{12} }·y = {c_1} \\ II. & {a_{21} }·x + {a_{22} }·y = {c_2} \end{array} \)
Gesucht sind wie im obigen Beispiel die Werte für x und y, bei denen sich beide Geraden schneiden. Beim Vergleich der Lösungen für x und y (vergleiche Gleichungen 62 und 63) fallen gewisse Gemeinsamkeiten auf:
• Die Nenner beider Bestimmungsgleichungen sind identisch,
• Die Zähler sind prinzipiell gleich.
Daher werden Möglichkeiten zur Formalisierung der Lösungsprozedur gesucht.
Zweireihige Determinanten
Determinanten sind schematisierte lineare Gleichungssysteme. Ziel dabei ist, mittels formalisierter Rechenschritte zu schnelleren Lösungen zu kommen.
Folgende Vereinbarungen gelten (siehe Abbildung):
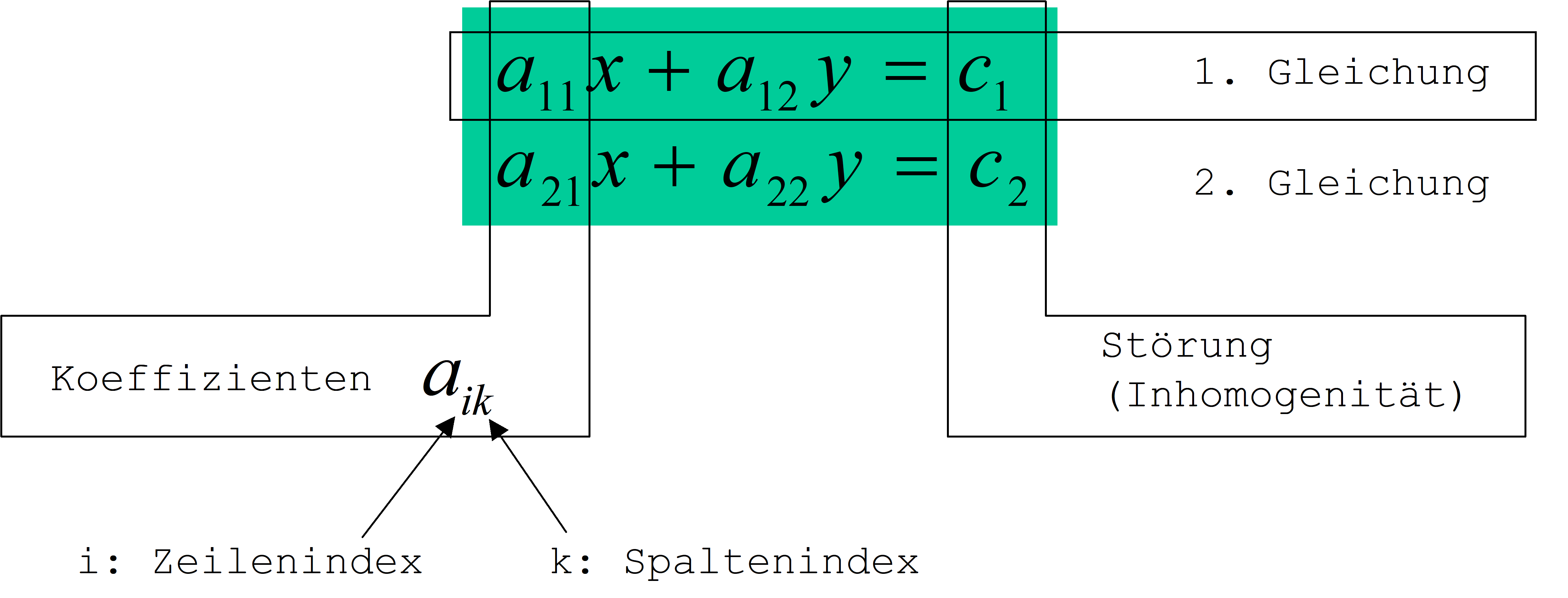
• Die Koeffizienten werden nach ihrer Stellung im Gleichungssystem benannt. Der Zeilenindex i steht vor dem Spaltenindex k.
• Die absoluten Glieder ci des Gleichungssystems werden auch als Störung oder Inhomogenität bezeichnet. Verschwinden die absoluten Glieder insgesamt, liegt ein homogenes andernfalls ein inhomogenes Gleichungssystem vor.

Die linke Seite des Gleichungssystems wird schematisch als sogenannte Determinante angeordnet, indem nur die Koeffizienten des Gleichungssystems vorzeichenbehaftet in ein quadratisches Schema angeordnet werden (siehe Gl. 64).
Für die Bestimmung des Wertes einer zweireihigen Determinante gilt als Rechenvorschrift:
Der Wert einer zweireihigen Determinante D ergibt sich aus dem Produkt der Koeffizienten der Hauptdiagonalen vermindert um das Produkt der Koeffizienten der Nebendiagonalen.
\( \left| { \begin{array}{cc}{ {a_{11} } } & { {a_{12} } } \\ { {a_{21} } } & { {a_{22} } } \end{array} } \right| = {a_{11} }·{a_{22} } - {a_{21} }·{a_{12} } = D \) Gl. 64
Ein Vergleich mit den Lösungsgleichungen 62 und 63 zeigt, dass der Wert der Determinante genau den Nennern der beiden Gleichungen entspricht. Da diese Determinante aus allen Koeffizienten des Gleichungssystems gebildet wird, heißt sie auch Koeffizientendeterminante.
Wird nun das Schema der Koeffizientendeterminante auf die Zähler der Lösungsgleichungen übertragen, so findet man mit:
\( \left| { \begin{array}{ cc}{ \textcolor{#F00}{c_1} } & { {a_{12} } } \\ { \textcolor{#F00}{c_2} } & { {a_{22} } } \end{array} } \right | = {c_1}·{a_{22} } - {c_2}·{a_{12} } = {D_x} \) Gl. 65
den Zähler der Lösungsgleichung für die Unbekannte x und mit
\( \left| {\begin{array}{cc} { {a_{11} } } & { \textcolor{#00F}{c_1} } \\ { {a_{21} } } & { \textcolor{#00F}{c_2} } \end{array} } \right| = {c_2}·{a_{11} } - {c_1}·{a_{21} } = {D_y} \) Gl. 66
den Zähler der Lösungsgleichung für die Unbekannte y.
Um eine Zählerdeterminante zur Bestimmung einer Variablen zu erhalten, werden in der Koeffizientendeterminante die Koeffizienten genau dieser Variablen durch die entsprechenden Störglieder ersetzt. Der Wert einer Zählerdeterminante wird nach der gleichen Regel wie der Wert einer Koeffizientendeterminante bestimmt.
Sind aber c1 = c2 = 0 liegt ein homogenes Gleichungssystem vor. Die Lösungen für x und y sind = 0.
Geometrische Interpretation:
Die Konstanten c1 bzw. c2 bewirken die Nullpunktverschiebung (Störung) der Geraden I bzw. II. Verschwinden diese Konstanten, gehen beide Geraden durch den Ursprung des Koordinatensystems und schneiden sich dort. Folglich werden die Werte der Zählerdeterminanten gleich 0 sein und die Lösungen des Gleichungssystems verschwinden.
