Lesezeit: 2 min Lizenz BY-NC-SA

Die Regel von SARRUS stellt ein vereinfachtes Lösungsverfahren für dreireihige Determinanten dar.

Das Lösungsschema nach Sarrus sieht vor, dass die ersten beiden Spalten der Determinante rechts neben die Determinante kopiert werden. Dadurch ergibt sich ein Schema nach Abbildung 16.

Nunmehr können die Produkte der Elemente, die sich auf den drei Hauptdiagonalen befinden, summiert werden. Davon abzuziehen sind die Produkte der Elemente auf den drei Nebendiagonalen.

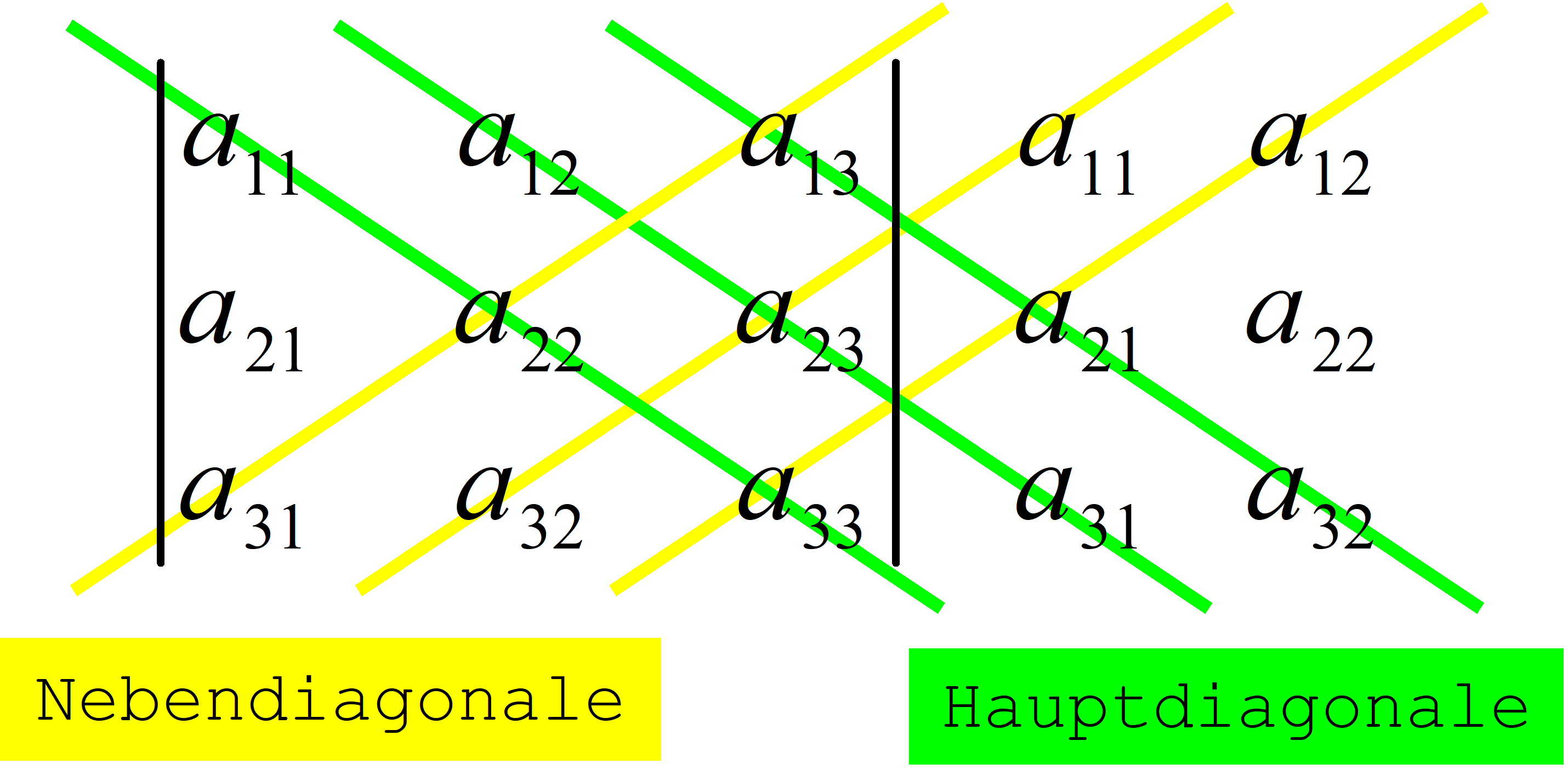
Abbildung 16 Schnittlinien der drei Flächen
Abbildung 16: Schnittlinien der drei Flächen

\( \left| {\begin{array}{cc}{ {a_{11} } }&{ {a_{12} } }&{ {a_{13} } } \\ { {a_{21} } }&{ {a_{22} } }&{ {a_{23} } } \\ { {a_{31} } }&{ {a_{32} } }&{ {a_{33} } } \end{array} } \right|\begin{array}{cc}{ {a_{11} } }&{ {a_{12} } } \\ { {a_{21} } }&{ {a_{22} } } \\ { {a_{31} } }&{ {a_{32} } } \end{array} = {a_{11} }{a_{22} }{a_{33} } + {a_{12} }{a_{23} }{a_{31} } + {a_{13} }{a_{21} }{a_{32} } - {a_{13} }{a_{22} }{a_{31} } - {a_{11} }{a_{23} }{a_{32} } - {a_{12} }{a_{21} }{a_{33} } \) Gl. 88


Kapitelübersicht:

  1. Geraden
  2. Schnittpunkt von Geraden
  3. Determinanten
  4. Cramersche Regel
  5. Deutigkeit von Lösungen zweireihiger Determinanten
  6. Eigenschaften zweireihiger Determinaten
  7. Gleichungssysteme auf lineare Gleichungssysteme zurückführen
  8. Drei- und mehrreihige Determinanten
  9. Regel von Sarrus
  10. Entwickeln einer Determinante nach ihren Unterdeterminanten (Adjunkte)
  11. Rang einer Determinante
  12. Eigenschaften drei- und mehrreihiger Determinanten
  13. Rändern von Determinanten
  14. Alternative Lösungsmethoden für Determinanten
  15. Erzeugen von nullwertigen Elementen
  16. Dreiecksdeterminanten
  17. Der Gauss’sche Algorithmus
  18. Gauß-Jordan-Algorithmus
  19. Anwendung von Determinanten